此题是群里崔老师分享的,抽时间整理下,难易适中,此类培优已经汇总一册,220题左右,答案几乎详解。
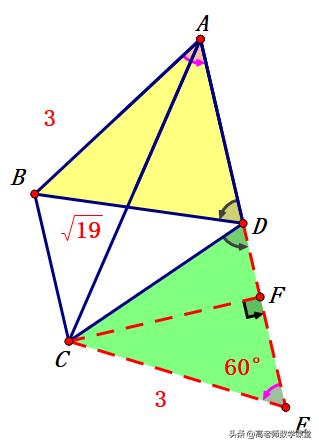
我们先看下题目:整理不易,大家多支持

解法一:
解:延长AD至点E,使得DE=DA
∵∠ADB ∠ADC=180°,∠EDC ∠ADC=180°
∴∠ADB=∠EDC
∵BD=CD,AD=ED
∴△ADB≌△EDC
∴AB=EC=3,∠BAD=∠E=60°
过点C作CF⊥AE
∵CE=3,∠E=60°
∴EF=(3/2),CF=(3√(3)/2)
在Rt△ACF中,AF(^2) CF(^2)=AC(^2)
∴AF=(7/2)
∴AE=5
∴DE=(5/2)
∴DF=1
在Rt△CDF中,CF(^2) DF(^2)=C(D^2)
∴CD=(√(31)/2)
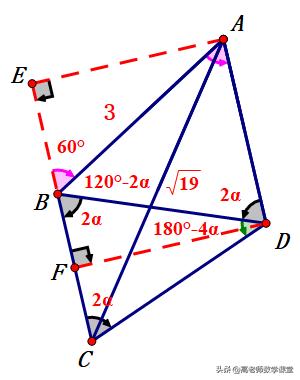
解法二:
解:设∠ADB=2α
∵∠ADB ∠ADC=180°
∴∠ADB ∠ADB ∠BDC=180°
∴∠BDC=180°-4α
∵BD=CD
∴∠DBC=∠DCB=2α
∵∠BAD=60°
∴∠ABD=120°-2α
∴∠ABC=120°
∵∠ADB=∠DBC=2α
∴AD∥BC
过点A作AE⊥CB,交CB延长线于点E
∵AB=3,∠ABE=60°
∴BE=(3/2),AE=(3√(3)/2)
在Rt△AEC中,AE(^2) CE(^2)=AC(^2)
∴CE=(7/2)
∴BC=2
过点D作DF⊥BC
∴CF=1,DF=(3√(3)/2)
在Rt△DFC中,D(F^2) CF(^2)=DC(^2)
∴CD=(√(31)/2)
全等及勾股定理是八年级学的知识,此类题的视频八年级三角形能力题绝大部分都是
几何填空压轴题:视频专栏,都是此类的几何培优题讲解,目前有90题左右
初中数学研究免费交流圈子:欢迎加入
,




