ARMA模型、ARIMA模型及季节模型,这些模型一般都假设干扰项的方差为常数,然而很多情况下时间序列的波动有集聚性等特征,使得方差并不为常数。因此,如何刻画方差是十分有必要研究的。本文介绍的ARCH、GARCH模型可以刻画出随时间变化的条件异方差。
参考文献1.《金融时间序列分析》 第2版 Ruey S.Tsay著 王辉、潘家柱 译2.TimeSeriesAnalysisTsa http://nipy.bic.berkeley.edu/nightly/statsmodels/doc/html/tsa.html3.Python arch 3.2 https://pypi.python.org/pypi/arch
七、自回归条件异方差模型(ARCH)7.1 波动率的特征对于金融时间序列,波动率往往具有以下特征:
(1)存在波动率聚集现象。即波动率在一段时间上高,一段时间上低。
(2)波动率以连续时间变化,很少发生跳跃
(3)波动率不会发散到无穷,波动率往往是平稳的
(4)波动率对价格大幅上升和大幅下降的反应是不同的,这个现象为杠杆效应
7.2 ARCH的基本原理在传统计量经济学模型中,干扰项的方差被假设为常数。但是许多经济时间序列呈现出波动的集聚性,在这种情况下假设方差为常数是不恰当的。
ARCH模型将当前一切可利用信息作为条件,并采用某种自回归形式来刻划方差的变异,对于一个时间序列而言,在不同时刻可利用的信息不同,而相应的条件方差也不同,利用ARCH模型,可以刻划出随时间而变异的条件方差。
7.2.1 ARCH模型思想1.资产收益率序列的扰动{at}是序列不相关的,但是不独立。
2.{at}的不独立性可以用其延迟值的简单二次函数来描述。
具体而言,一个ARCH(m)模型为:

从上面模型的结构看,大的过去的平方“扰动”会导致信息at大的条件异方差。从而at有取绝对值较大的值的倾向。这意味着:在ARCH的框架下,大的"扰动"会倾向于紧接着出现另一个大的"扰动"。这与波动率聚集的现象相似。
所谓ARCH模型效应,也就是条件异方差序列的序列相关性
7.3 ARCH模型建立ok,上面尽可能简单的介绍了ARCH的原理,下面主要介绍如何python实现。ARCH模型建立大致分为以下几步:
步骤(1):通过检验数据的序列相关性建立一个均值方程,如有必要,对收益率序列建立一个计量经济模型(如ARMA)来消除任何线形依赖。
步骤(2):对均值方程的残差进行ARCH效应检验
步骤(3):如果具有ARCH效应,则建立波动率模型
步骤(4):检验拟合的模型,如有必要则进行改进
arch库其实提供了现成的方法(后面会介绍),但是为了理解ARCH,我们按流程来建模
7.3.1 均值方程的建立这里的均值方程可以简单认为建立ARMA(或ARIMA)模型,ARCH其实是在此基础上的一些“修正”。我们以上证指数日涨跌幅序列为例:
由于后面的arch库均值方程只支持常数、零均值、AR模型,我们这里建立AR模型,方便对照~
# 相关库
from scipy import stats
import statsmodels.api as sm # 统计相关的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import arch # 条件异方差模型相关的库
IndexData = DataAPI.MktIdxdGet(indexID=u"",ticker=u"000001",beginDate=u"20140101",endDate=u"20160101",field=u"tradeDate,closeIndex,CHGPct",pandas="1")
IndexData = IndexData.set_index(IndexData['tradeDate'])
data = np.array(IndexData['CHGPct']) # 上证指数日涨跌
IndexData['CHGPct'].plot(figsize=(15,5))

首先检验平稳性,是否需要差分。原假设H0:序列为非平稳的,备择假设H1:序列是平稳的
t = sm.tsa.stattools.adfuller(data) # ADF检验
print "p-value: ",t[1]
p-value: 7.55775720826e-10
p-value小于显著性水平,拒绝原假设,因此序列是平稳的,接下来我们建立AR(p)模型,先判定阶次
fig = plt.figure(figsize=(20,5))
ax1=fig.add_subplot(111)
fig = sm.graphics.tsa.plot_pacf(data,lags = 20,ax=ax1)

于是我们建立AR(8)模型,即均值方程
order = (8,0)
model = sm.tsa.ARMA(data,order).fit()
我们利用(一)中的混成检验(Ljung-Box),检验序列 {a2t} 的相关性,来判断是否具有ARCH效应
计算均值方程残差:
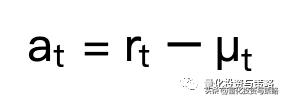
画出残差及残差的平方
at = data - model.fittedvalues
at2 = np.square(at)
plt.figure(figsize=(10,6))
plt.subplot(211)
plt.plot(at,label = 'at')
plt.legend()
plt.subplot(212)
plt.plot(at2,label='at^2')
plt.legend(loc=0)
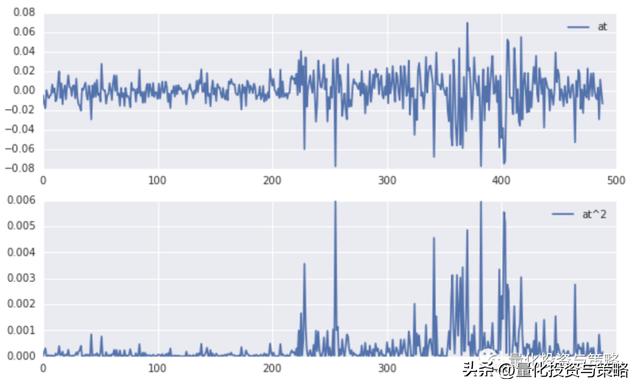
然后对{a2t}序列进行混成检验:原假设H0:序列没有相关性,备择假设H1:序列具有相关性
m = 25 # 我们检验25个自相关系数
acf,q,p = sm.tsa.acf(at2,nlags=m,qstat=True) ## 计算自相关系数 及p-value
out = np.c_[range(1,26), acf[1:], q, p]
output = pd.DataFrame(out, columns=['lag', "AC", "Q", "P-value"])
output = output.set_index('lag')
output

p-value小于显著性水平0.05,我们拒绝原假设,即认为序列具有相关性。因此具有ARCH效应。
7.3.2 ARCH模型的建立首先讲讲ARCH模型的阶次,可以用{a2t}序列的偏自相关函数PACF来确定:
fig = plt.figure(figsize=(20,5))
ax1=fig.add_subplot(111)
fig = sm.graphics.tsa.plot_pacf(at2,lags = 30,ax=ax1)

由上面的图我们可以粗略定为4阶。然后建立AR(4)模型
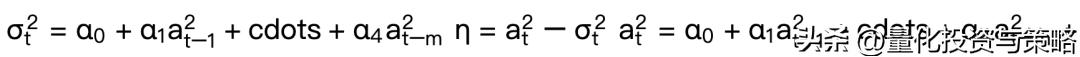

后续的AR模型就不建立了~ 当然,按照上述流程走下来非常麻烦~
事实上arch库可以一步到位~:
根据我们之前的分析,可以粗略选择均值模型为AR(8)模型,波动率模型选择ARCH(4)模型
train = data[:-10]
test = data[-10:]
am = arch.arch_model(train,mean='AR',lags=8,vol='ARCH',p=4)
res = am.fit()

res.summary()
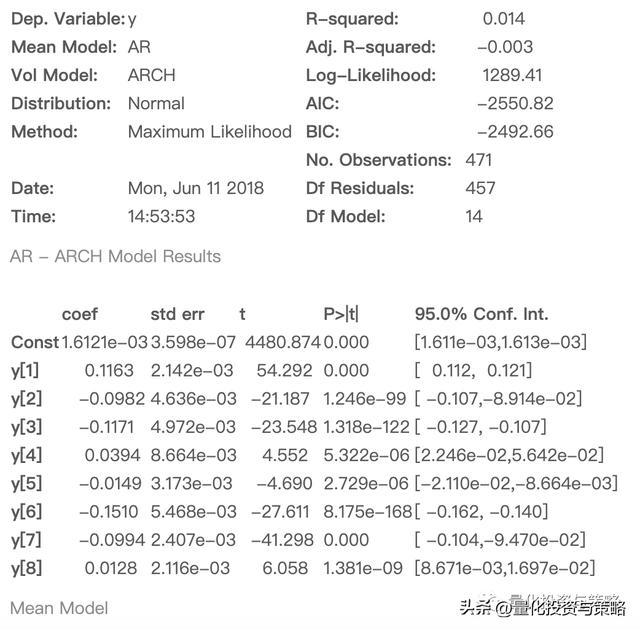

res.params

可以看出,我们的模型为:

对上述模型,我们可以看出,上证指数的日收益率期望大约在0.16%。模型的R-squared较小,拟合效果一般。
7.3.3 ARCH模型的预测首先来看整体的预测拟合情况:
res.hedgehog_plot()

可以看出,虽然具体值差距挺大,但是均值和方差的变化相似。下面再看最后10个数据的预测情况
len(train)
479
pre = res.forecast(horizon=10,start=478).iloc[478]
plt.figure(figsize=(10,4))
plt.plot(test,label='realValue')
pre.plot(label='predictValue')
plt.plot(np.zeros(10),label='zero')
plt.legend(loc=0)

可以看出,光从看涨看跌的角度去看,预测看涨看跌的正确率为60%,当然,其实模型更重要的功能是预测波动率。
八、GARCH模型与波动率预测虽然ARCH模型简单,但为了充分刻画收益率的波动率过程,往往需要很多参数,例如上面用到ARCH(4)模型,有时会有更高的ARCH(m)模型。因此,Bollerslev(1986)年提出了一个推广形式,称为广义的ARCH模型(GARCH)
另

为t时刻的新息。若at满足下式:

其中,εt为均值为0,方差为1的独立同分布(iid)随机变量序列。通常假定其服从标准正态分布或标准化学生-t分布。σ2t为条件异方差。
则称at服从GARCH(m,s)模型。仔细观察公式,发现与ARMA模型很相似!
8.1 GARCH模型建立与之前的ARCH模型建立过程类似,不过GARCH(m,s)的定阶较难,一般使用低阶模型如GARCH(1,1),GARCH(2,1),GARCH(1,2)等。
下面我们以之前的数据为例,构建GARCH模型,均值方程为AR(8)模型,波动率模型为GARCH(1,1)
train = data[:-10]
test = data[-10:]
am = arch.arch_model(train,mean='AR',lags=8,vol='GARCH')
res = am.fit()

res.summary()

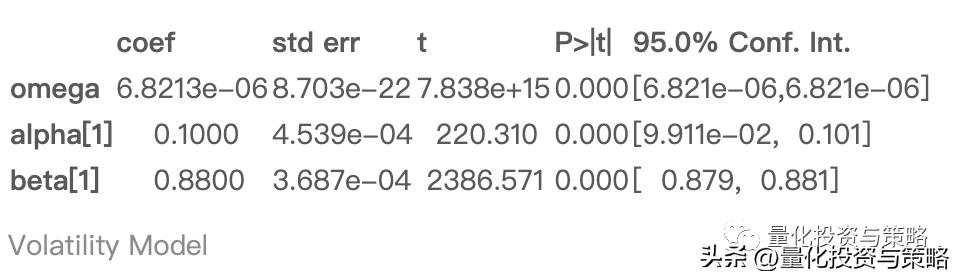
res.params

我们得到波动率模型:

res.plot()
plt.plot(data)

观察上图,第一张图为标准化残差,近似平稳序列,说明模型在一定程度上是正确的;
第二张图,绿色为原始收益率序列、蓝色为条件异方差序列,可以发现条件异方差很好得表现出了波动率。
res.hedgehog_plot()

观察拟合图发现,在方差的还原上还是不错的。
8.2 波动率预测上一章的预测直接预测了收益率,然而直接预测收益率准确度并不是很高,因此很多时候我们主要用来预测波动率,根据上面建立的波动率模型:

我们可以按照我们建立好的模型一步步计算。
根据模型:
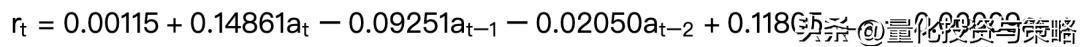
先计算at的预测值
res.params

我们需要提取均值方程的系数向量w,再逐个计算at后面10个值
ini = res.resid[-8:]
a = np.array(res.params[1:9])
w = a[::-1] # 系数
for i in range(10):
new = test[i] - (res.params[0] w.dot(ini[-8:]))
ini = np.append(ini,new)
print len(ini)
at_pre = ini[-10:]
at_pre2 = at_pre**2
at_pre2

接着根据波动率模型预测波动率:

ini2 = res.conditional_volatility[-2:] #上两个条件异方差值
for i in range(10):
new = 0.000007 0.1*at_pre2[i] 0.88*ini2[-1]
ini2 = np.append(ini2,new)
vol_pre = ini2[-10:]
vol_pre
array([ 0.01371481, 0.01211263, 0.01066613, 0.00939748, 0.00828216, 0.00729652, 0.00651609, 0.00575681, 0.0050735 , 0.00448723])
我们将原始数据、条件异方差拟合数据及预测数据一起画出来,分析波动率预测情况
plt.figure(figsize=(15,5))
plt.plot(data,label='origin_data')
plt.plot(res.conditional_volatility,label='conditional_volatility')
x=range(479,489)
plt.plot(x,vol_pre,'.r',label='predict_volatility')
plt.legend(loc=0)

可以看出,对于接下来的1、2天的波动率预测较为接近,然后后面几天的预测逐渐偏小。
可惜的是arch库中没有找到直接调用的方法,只好自己来计算。
小结本篇是金融时间序列系列的最后一篇,重点还是在基础的概念和python实现上。事实上要真学好这些模型,少不了更多的参考和实验。
另外,还有很多扩展的或改进的模型如求和GARCH、GARCH-M模型、指数GARCH、EGARCH模型等等。 对于波动率模型,还有比较常用的有随机波动率模型等, 有兴趣可以去研究下。
,




