古希腊数学家说过,哪里有数学,哪里就有美。《数学课程标准》指出:"数学是人类文化的重要组成部分,数学素质是公民所必须具备的一种基本素质。通过在中学阶段数学文化的学习,学生将初步了解数学科学与人类社会发展之间的相互作用,体会数学的科学价值、应用价值、人文价值,开阔视野,寻求数学进步的历史轨迹,激发对数学创新原动力的认识,受到优秀文化的熏陶,领会数学的美学价值,从而提高数学的文化素养和创新意识。"这就要求我们的课堂教学要结合具体的数学内容,有效的渗透数学文化,提高学生的数学素质。下面以毕达哥拉斯树为例说说数学文化的魅力。

虽说数学是十分枯燥的,但是科学家总能从中找到无限的乐趣,毕达哥拉斯树就是由古希腊数学家毕达哥拉斯,利用勾股定理所画出的一个无限重复图形,当重复的次数够多时,就会形成一个树的形状,所以也有人称之为"勾股树"。
勾股树的相关结论:
(1).两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。
(2).三个正方形之间的三角形,其面积小于等于大正方形面积的四分之一,大于等于一个小正方形面积的二分之一。

众所周知勾股定理就是直角三角形的两个直角边的平方和,等于斜边的平方,毕达哥拉斯利用这一点,在初始的大正方形上,做出了两个全等的小正方形,在以此类推,无限重复的做出各种大小不一的正方形,就形成了茂密的"毕达哥拉斯树"。
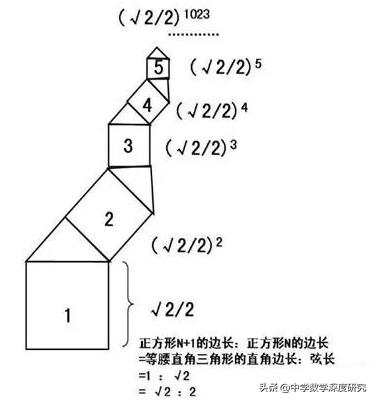
由于三个正方形的内部形成了一个等腰直角三角形,所以通过勾股定理可得,小正方形的边长是大正方形的√2/2,在通过对小正方形重复上述过程,无限重复下去。如果假设其中的大正方形边长为1,在增加到第n 次时,会增加2n个小正方形,而每个小正方形的边长就是√2/2,则每一次增加的面积就是2n×(½√2)=1。
从每一个图中两个较小的正方形出发,又可以分别作出一个第三代的勾股定理图(图4),就这样一生二、二生四、四生八,继续繁殖下去,就长成了图1那样的大树,整棵大树完全是由勾股定理图形组成的,把它叫做勾股树,名副其实,非常恰当。
通过改变第一代勾股定理图中直角三角形三边的比例,或者在繁殖过程中适当改变两条直角边的方向,可以得到不同图形的勾股树,就是另外一幅美丽的勾股树形图。 变形啦!变形啦!“妖树”变形啦!

用GeoGebra绘制的勾三股四弦五勾股树,它美丽,它漂亮;它象征着生活多姿多彩,数学五彩斑斓;它孕育着人生勇攀高峰,学问永无止境……
3. 毕达哥拉斯树是无限的吗?传说毕达哥拉斯树的树种一旦扎根于土中,第一年吸收10点能量破土而出1个方块木桩,第二年又吸收10点能量抽出2块方块木枝,第三年又吸收10点能量发出4块方块树芽,第四年有吸收10点能量长出8块方块树枝,……,此后每一年都会吸收等量的能量向外发出更多更细小的方块枝条.你能想象那是怎样一幅绝景吗?
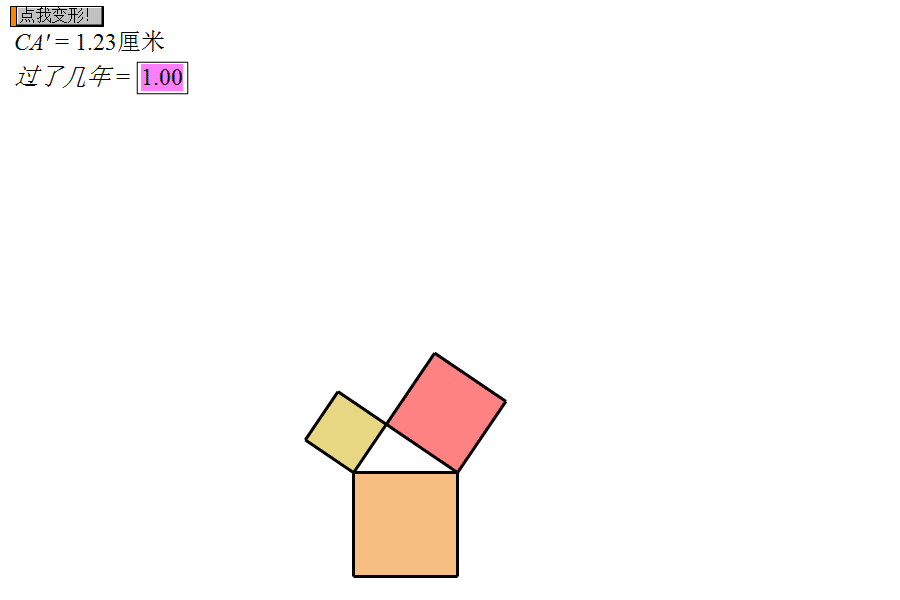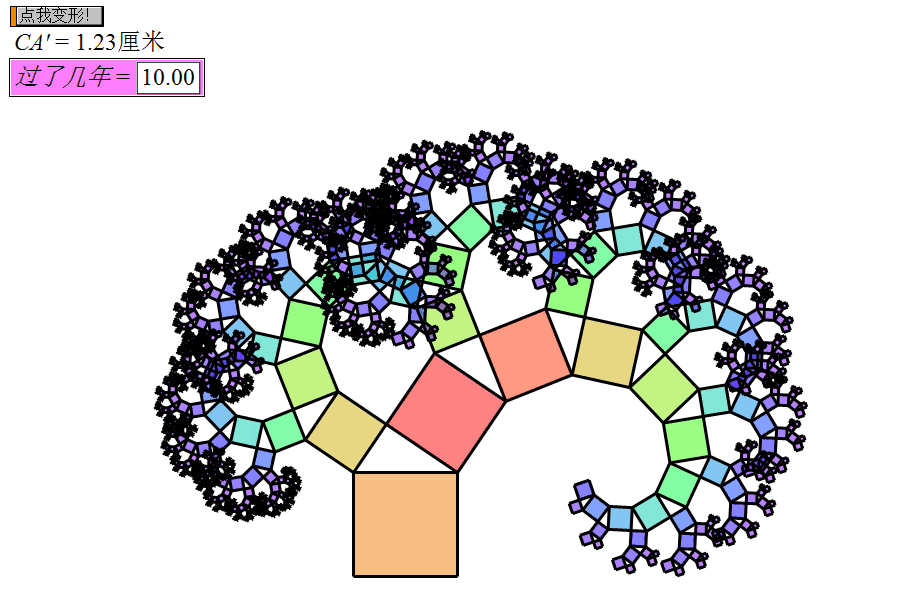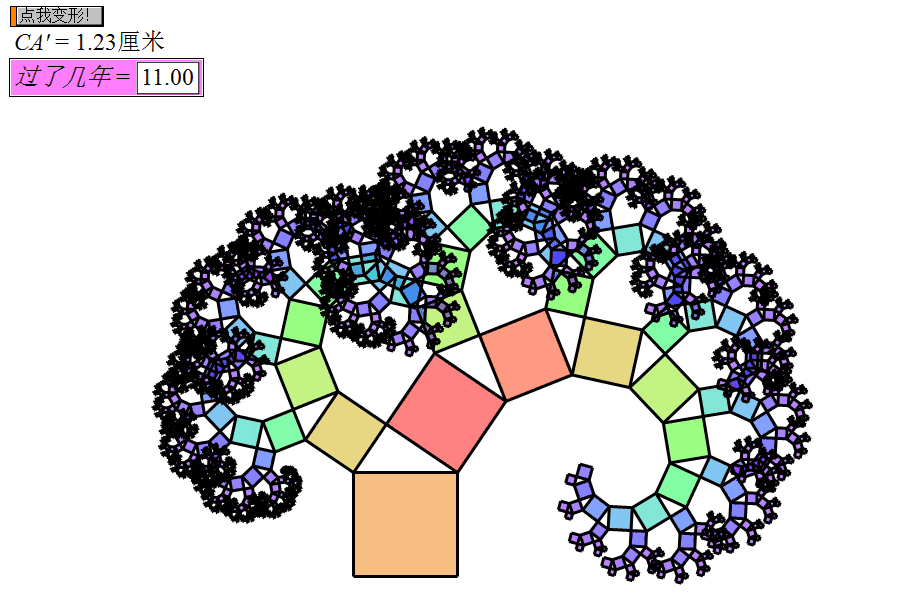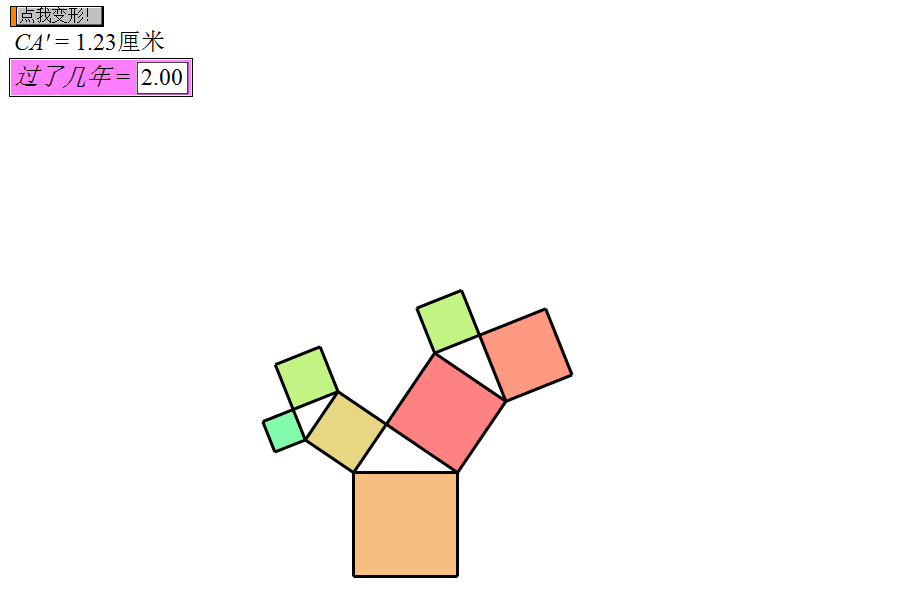
理论上来看,毕达哥拉斯树是可以无限重复的,因为将上诉的公式中的n设为无限次后,毕达哥拉斯树的面积就会趋于无限大。勾股树的面积也会更加茂密,但是在现实中并非如此。
因为当n大于5时,所有产生的小正方体互相重叠,所以毕达哥拉斯树的面积其实是有限的。因此毕达哥拉斯树其实只能生长在一个6×4的方格中里,当然具体的值不太容易求出。
4.毕达哥拉斯树的变种最初的毕达哥拉斯树中的大正方形和小正方形夹角是不等的,所以有一种毕达哥拉斯树的变种就是改变夹角,当最开始的大正方形和小正方形之间的夹角变为60度时,中间的三角形就会变成等边三角形,这样每一个正方形的边长都是相等的。
但是这种变种也和正常的毕达哥拉斯树一样,是有限的,达到第四步的时候就会发生重叠,最后就会形成一个大六边形,里面全是边长相等的正方形。

知微见著,窥一斑而见全豹,我们应该实现数学文化和人类文明的整合,要搞清楚数学的文化背景,搞清楚数学成就的文化价值,把数学结果的文化品位发掘出来,用文化的视野来看数学, 用数学的眼光来看文化,发展现代数学,弘扬世界的文化。

罗素曾这样评价数学:如果正确地看它,不但拥有真理,而且也具有至高的美,正像雕刻的美,是一种冷而严肃的美。让我们以数学文化为平台,化"冰冷的魅力"为"火热的思考"!
,