
导数
学习导数,首先需要确定的是导数的本质,导数的本质在于:导数的值反映了原函数的函数值变化的快慢程度,导数的符号反映了原函数的函数值变化方向。
于是,原函数的函数值在某区间内变化越快,其在该区间上的导数绝对值也就越大;原函数的函数值在某区间内变化越慢,其在该区间上的导数绝对值也就越大。
此外,导数的符号反映的是原函数的函数值如何变化,导数大于0,则原函数的函数值在自变量区间内递增,导数小于0,则原函数的函数值在自变量区间内递减。
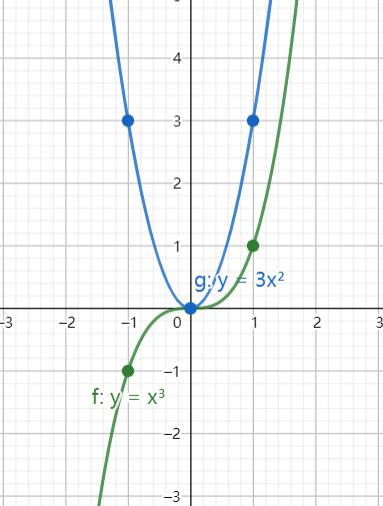
示例
导数运算公式:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
需要注意,在上述式子中,并不是关于的函数。以上十二个导数运算公式需要牢牢记住,在需要使用的时候及时用上就行。
导数运算法则:
(1)
(2)
(3)
需要注意,在上述式子中,和都是关于的函数,因此才可以对和求导。以上三条导数运算法则同样需要牢牢记住。
复合函数链式法则:
链式法则是导数学习中最重要的法则,熟练使用链式法则可以删繁就简,推导出一些复杂函数的导数。在数学计算的过程中,应尽量将复杂问题简单化,链式法则就是一个这样的工具。
对于复合函数的导数,需要注意的是,分母是一个函数,所以求导时需要使用上链式法则。
下面再使用链式法则来推导第(3)条导数运算法则:
欢迎关注、转发、收藏!
,




