
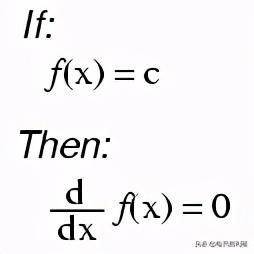
(“c”为常数)
常见衍生工具

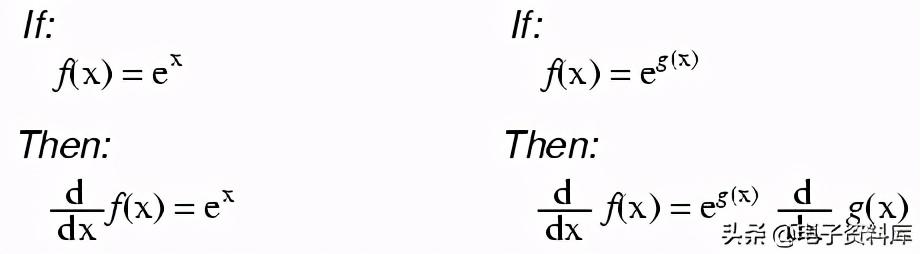

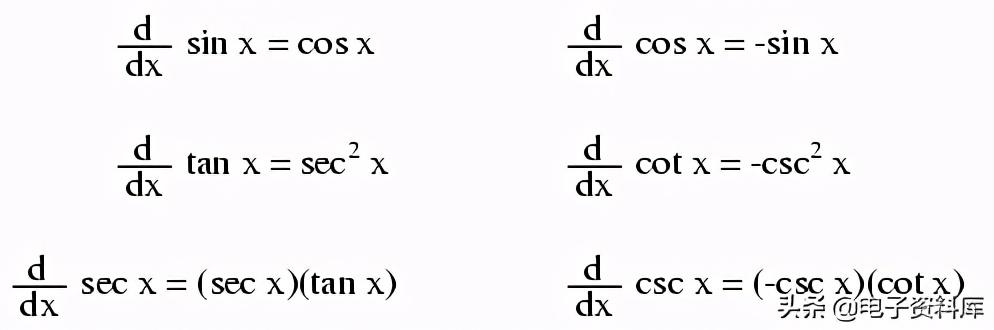








注意这里重要的一点:取f(x)的导数可以精确地得到g(x),但是使用g(x)的反导数并不一定给出f(x)的原始形式。例子:

注意常数c是未知的!原始函数f(x)可能是3x two5,3倍 two10,3倍 two 任何东西,而f(x)的导数仍然是6x,那么确定函数的反导数要比确定函数的导数要少一些。
常用抗蚀剂



注:这是e的一个非常独特和有用的性质,和导数一样,这种函数的反导数也是同一个函数。在反除法的情况下,在末尾加上一个常量“c”。
反兴奋剂规则常数规则
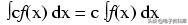




与法方程的解是一个数不同,微分方程是一个解实际上是一个函数,并且该未知函数的至少一个导数是方程的一部分。
与寻找函数的反导数一样,我们通常会得到一个包含多种可能性的解决方案(考虑反导数中常见的常数“c”的许多可能值)。回答任何微分方程的函数集称为该微分方程的“通解”。这个集合中的任何一个函数都被称为该微分方程的“特定解”。微分方程中微分和积分的参考变量称为“自变量”
,




