1
类型4:含f(x) (或-)f'(x)tanx类

解析:这里f'(x)sin2x 2f(x)cos2x>0很容易构造出原函数g(x)=f(x)sin2x;
因为f(x)为奇函数,sin(2x)为奇函数,根据结论奇函数乘奇函数=偶函数,所以g(x)为偶函数。
又因为x属于(0,2分子派)时,导数大于0,原函数单调递增,所以根据对称性,画出g(x)图像。
它这里需要找出g(x)<1的x的范围,因此我们先来找x=多少时,g(x)=1,把x=8分之派利用起来,g(8分之派)=1,由偶函数对称性,g(-8分之派)=1
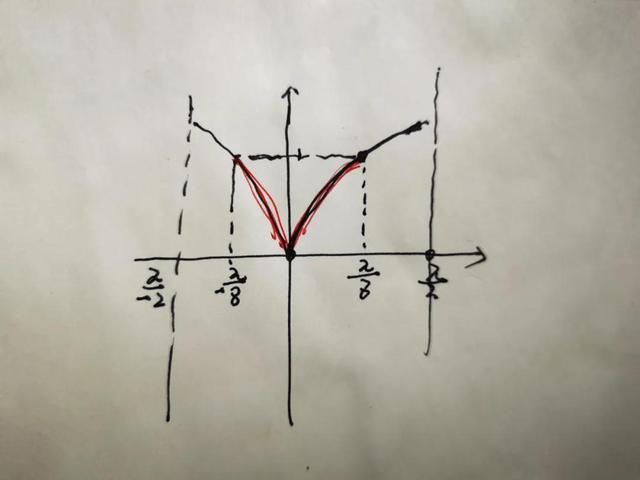
所以x属于(-8分之派,8分之派)
2
方法技巧:
在(0,2分子派)上,[sinx乘f(x)]’=cosx乘f(x) sinx乘f(x),其符号与f(x) f'(x)tanx相同;

,其符号与
f(x)-f'(x)tanx相同,在含有f(x) (或-)f'(x)tanx的问题中,可以考虑构造函数g(x)=f(x)sinx,h(x)=f(x)/sinx等
3
视频讲解
这样我们以4期来讲面对不同导数情况时,怎么来构造原函数,怎么来解决不等式问题。大家有什么疑惑,均可发送给我。
中学数学有什么需要帮助的,可以关注我的公粽号“高中数学谭老师”,或者私信问我,都能帮助你,使你数学得到提升。
,




