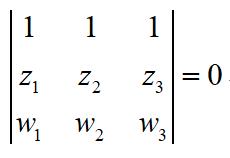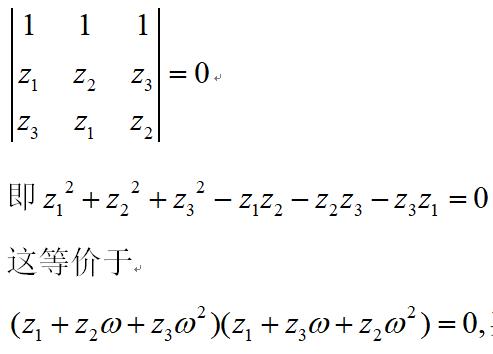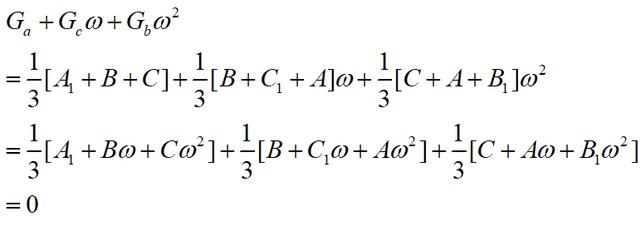根据谈数论理网友的建议做了修正
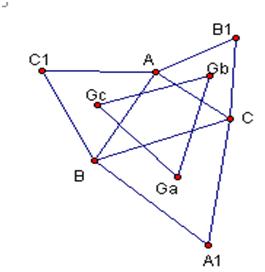
拿破仑定理拿破仑定理是法国著名的军事家拿破仑·波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边,向外构造三个等边三角形,则这三个等边三角形的重心恰为另一个等边三角形的顶点。”该等边三角形称为拿破仑三角形。如果向内作三角形,结论同样成立。
这篇短文讲述如何用复数证明这个定理。可以看成高中复数的扩展内容,是我用于高中数学竞赛训练扩展思路的材料。可做为教竞赛或者教想考好大学的老师教学,以及优秀的高中同学学习参考。
1.复平面的三点比-预备知识我们知道,复数是复平面的一个点。设三个复数z1,z2,z3,可以定义三点比为
V(z1,z2,z3)=( z2- z1)/ ( z3- z1). 三点比V(z1,z2,z3)是个复数,其复角就是复平面上⊿z2z1z3中∠z2z1z3的有向大小。而模是边z1 z2与z1 z3的长度比。角度相等对应边成比例,在平面几何中是三角形相似的判别条件。而在复平面上,⊿z1z2z3∽⊿w1w2w3等价于
V(z1,z2,z3)= V( w1,w2,w3)。。。。。(1)
(1)展开的话,不难看出也可以写成行列式:
利用相似,我们来看正三角形⊿z1z2z3的判据:对于正三角形来说:由于z1z2z3∽⊿z3z1z3,就有:
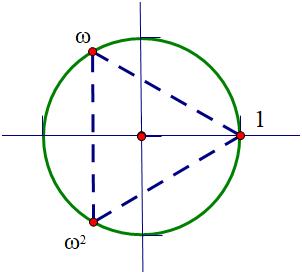
对于看不懂行列公式的同学,(1)式的右边直接拿1,ω,ω2替换w1,w2,w3也不难得到一般三角形与正⊿1ωω2相似的判定条件
拿破仑定理的证明
图1
图2
证明:⊿A1BC∽⊿1ωω2,⊿BC1A∽⊿1ωω2,⊿CAB1∽⊿⊿1ωω2
由复平面正三角形相似条件,就有:
下面计算
,