

许兴华数学(图片来自万邦朝圣,特此感谢!)
众所周知,在高中数学学习过程中,如果学习到“椭圆、双曲线、抛物线”(简称为圆锥曲线)这一内容时,为了加深学生对圆锥曲线三个定义的理解,教师一般都要做出这三种图形。而作出这三种圆锥曲线图形的有效方法,目前比较流行的当然是运用“几何画板”方法(这个方法,教师在课堂上可以分别演示给学生观看),但在上课时,由于并不是每个学生都有一台电脑,所以我们教师就做不到,让人人动手来亲自画圆锥曲线。
有鉴于此,今天,我们就建议各位老师给学生来一个“奇妙一招”:如何用“尺规作图”作出椭圆、双曲线和抛物线?用尺规作图来作做圆锥曲线的图形,效果是显而易见的:每个人都可以有圆规和三角板,在课堂上能做到让全班同学人人动手,这对学生深刻理解三种“圆锥曲线”的定义是有非常大的帮助的。
(首先,大家须记住:“尺规作图”是指用圆规和没有刻度的直尺来作几何图形的一种方法)
【一】用尺规作图作出椭圆(基本步骤和方法)
1、先作出两条互相垂直的直线分别作为x轴和y轴,它们的交点为原点O,任意给出两条线段AB=2a,EF=2c(a>c>0),(此时E、F即为椭圆的两个焦点),在x轴上依次截取OA=OB=a,OE=OF=c.于是,得到点A、B是椭圆上的两个点;
2、在线段EF上任取一点C,以E为圆心、AC为半径画圆C,以F为圆心、BC为半径画圆F,两圆相交于G、H两点,则又得到椭圆上的两点G,H(如下图1)。

3、在线段EF上任取另一点J,以E为圆心、AJ为半径画圆E,以F为圆心、BJ为半径画圆F,两圆相交于I、K两点,则又得到椭圆上的两点I,K(如下图2)。

4.在线段EF上,模仿步骤3,不断地改变J点的位置,依照上面方法可画出椭圆上其它的点L、M,......,(如图3,图4)


5.用光滑的曲线依次把以上得到的点A、G、I、L、H、K、M,......连结起来,我们就得到了所要作的椭圆的图形(如图4).
证明从略,请读者自己证明一下。
【二】用尺规作图作出双曲线(基本步骤和方法)
1、先作出两条互相垂直的直线分别作为x轴和y轴,它们的交点为原点O,任意给出两条线段AB=2a,EF=2c(c>a>0),在x轴上依次截取OA=OB=a,OE=OF=c.(其实,E、F即为两个焦点)。于是,得到点A、B是双曲线上的两个点;
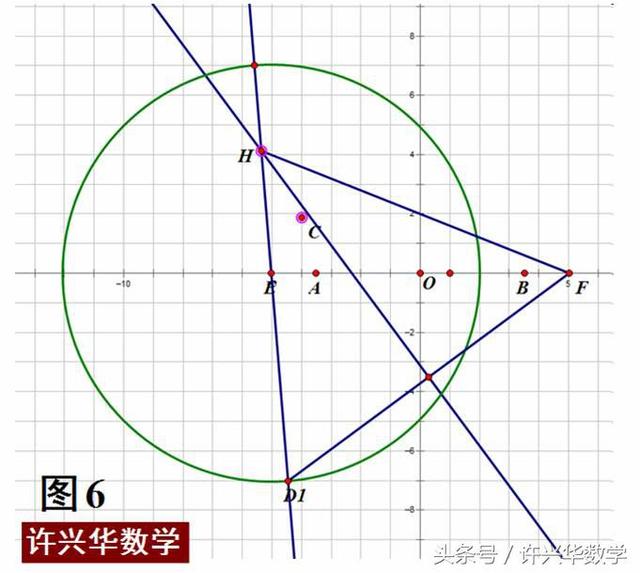
2、以E为圆心、2a为半径画圆E,过点E任意作一条直线CD交圆E于一点D,连结DF,作DF的垂直平分线交直线DE于C点,则又得到双曲线上的一点C(如下图5);

3.模仿上面步骤2,不断地改变D点的位置为D1,D2,D3,......,依照上面方法可画出双曲线上其它的点H、L,......,(如图6,图7)

4.用光滑的曲线依次把以上得到的点A、G、I、L、H、K、M,......连结起来,我们就得到了所要作的双曲线左支的图形(如图8).
5.完全类似于以上的步骤和方法可画出双曲线的右支(如图8).
证明从略,请读者自己证明一下。

【三】用尺规作图作出抛物线(基本步骤和方法)
1、由抛物线的定义知,抛物线上任意一点B到定点F和定直线L的距离相等。我们先作出一个定点F和一条定直线L(定点F不在定直线L上),过点F作L的垂线,垂足为A1,再取线段FA1的中点B1,于是,得到点B1是抛物线上的一个点;

2、在直线L上任意取一个异于点A1的点A2,连结FA2,作线段FA2的垂直平分线交过A2而平行于x轴的直线于点B2,连结FB2,则又得到抛物线上的一点B2(如上图9);
3.模仿上面步骤2,不断地改变A2点的位置为A3,A4,A5,......,依照上面方法可画出抛物线上其它的点B3、B4,B5......,(如图9)
4.用光滑的曲线依次把以上得到的点B1、B2、B3、B4、B5、B6、......连结起来,我们就得到了所要作的抛物线的图形(如图9).
证明从略,请读者自己证明一下。

许兴华数学(网络配图)
,




