一.对“对应”二字认识不准确,应用全等判别法有误
例1 △ABC 和 △DEF 中,∠A=30°,∠B=70°,AC=17cm,∠D=70°,∠E=
80°,DE=17cm.那么△ABC与△DEF全等吗?为什么?
错解:△ABC与△DEF全等.证明如下:
在△DEF中,
∵ ∠D=70°,∠E=80°,∴ ∠F=180°-∠D-∠E=180°―70°―80°=30°.
在△ABC中,
∵ ∠A=30°,∠B=70°,∴ ∠A=∠F,∠B=∠D.
又∵ AC=17cm,DE=17cm,∴ AC=DE .
在△ABC与△DEF中,
∴ △ABC≌△DEF.
错解分析:AC是∠B的对边,DE是∠F的对边,而∠B≠∠F,所以这两个三角形不全等.△ABC与△DEF不全等.因为相等的两边不是相等的两角的对边,不符合全等三角形的判别法.
二.判定方法有错误
例2 如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC.
求证:∠D=∠E.

错解:在△ACE与△BCD中,
∵AC⊥BC , DC⊥EC,
∴∠ACB=∠ECD=90°.
又∵AC=BC,DC=EC,
∴ △ACE≌△BCD,∴∠D=∠E.
错解分析:上面的证明中,错误地应用了“边角边”. ∠ACB与∠ECD并不是那一对三角形的内角.
正解:∵ AC⊥BC,DC⊥EC,
∴ ∠ACB=∠ECD=90°,
∴ ∠ACE=∠BCD.
∵ AC=BC, ∠ACE=∠BCD,DC=EC,
∴ △ACE≌△BCD, ∴∠D=∠E.
三.错误套用等式性质
例3 如图,已知AC,BD相交于E点,∠A=∠B, ∠1=∠2.
求证:AE=BE.
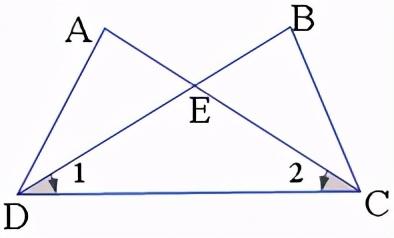
错证:在△ADC和△BCD中,
∵∠A=∠B,DC=CD, ∠2=∠1,
∴△ADC≌△BCD,
∴△ADC-△DEC=△BCD-△DEC,
∴△ADE≌△BCE, ∴AE=BE.
错解分析:在证明三角形全等时,一定要按判定定理进行证明.上面的证明中,将等式性质错误地搬到了三角形全等中.这是完全错误的.
正解:同上,易证△ADC≌△BCD,
∴AD=BC.
在△ADE和△BCE中,
∵AD=BC,∠A=∠B,∠AED=∠BEC,
∴△ADE≌△BCE,∴AE=BE.
四.脱离题设,将对图形的直观印象视为条件进行证明
例4 如图,在△ABC中,AD是它的角平分线,BD=CD.DE,DF分别垂直于AB,AC,垂足为E,F.
求证:BE=CF.

错解1:认为DE=DF,并以此为条件.
在Rt△BDE与Rt△CDF中,
∵DE=DF,BD=CD,
∴Rt△BDE≌Rt△CDF(斜边直角边),∴BE=CF.
错解2:认为AD⊥BC,并以此为条件.
通过证明△ABD≌△ACD(边角边),得AB=AC,再由△AED≌△AFD(角角边),得AE=AF,从而得到BE=CF.
错解分析:错解1中认为DE=DF,并直接将其作为条件应用,因而产生错误;
错解2中,认为AD⊥BC,没有经过推理加以说明,因而也产生了错误.产生上述错误的原因是审题不清,没有根据题设结合图形找到证题依据.
正解:在△AED和△AFD中,
∴ △AED≌△AFD(角角边),∴DE=DF.
在Rt△BDE与Rt△CDF中,
Rt△BDE≌Rt△CDF(斜边直角边),∴BE=CF.
五.误将“SSA (边边角)”当成“SAS (边角边)”来证题
例5 如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠ABE=∠ACE.
试证明:∠BAE=∠CAE.

错解:在△AEB和△AEC中,
∴ △AEB≌△AEC,
∴∠BAE=∠CAE.
错解分析:上解错在证两个三角形全等时用了“边边角”来判定,这是不正确的,因为有两条边以及其中一边的对角对应相等的两个三角形不一定全等.
正解:在△BEC中,因EB=EC,故∠EBC=∠ECB.
∵ ∠ABE=∠ACE, ∴∠ACB=∠ABC,∴AB=AC,
在Rt△AEB和Rt△AEC中,
∴△AEB≌△AEC,∴∠BAC=∠CAE.
在学习中,学会对题中图形进行观察以及对已知条件进行分析,弄明白证明思路.同时,对三角形全等的各种条件要记熟并能区分.三角形的全等具有传递性,比如若有△ABC≌△DEF,△DEF≌△MNP,则一定有△ABC≌△MNP,这个性质在解题时有很重要的应用.在一些计算图形中有几对全等三角形的题目时,利用这个性质可以发现一些不明显的全等关系,帮助发现那些不是直接有关联的全等三角形.
六.把“角角角”当成判定三角形全等的条件来使用
例6 如图, ∠CAB =∠DBA, ∠C=∠D, E为AC和BD的交点.△ADB与△BCA全等吗? 说明理由.

错解: △ADB ≌△BCA.
因为∠C = ∠D, ∠CAB = ∠DBA, 所以∠DAB =∠CBA,
所以△ADB ≌△BCA(AAA) .
错解分析: 错解把三个角对应相等作为这两个三角形全等的依据, 显然是错误的, “角角角”不是识别两个三角形全等的条件.
正解: △ADB ≌△BCA.
因为∠CAB = ∠DBA, ∠C = ∠D, AB = BA(公共边) ,
所以△ADB ≌△BCA(AAS) .
七.把“边边角”当成判定三角形全等的条件来使用
例7 如图,已知△ABC 中, AB = AC, D,E 分别是AB,AC 的中点, 且CD = BE,
△ADC 与△AEB全等吗? 说明理由.

错解: △ADC ≌ △AEB.
因为AB = AC, BE = CD, ∠BAE = ∠CAD,
所以△ADC ≌ △AEB(SSA) .
错解分析: 错解把“边边角”作为三角形全等的判别方法, 实际上, “边边角”不能作为三角形全等的判别依据, 因为两边及一边对角对应相等的两个三角形不一定全等.
正解: △ADC ≌ △AEB.
因为AB = AC, D,E 为AB,AC 的中点,
所以AD = AE.
在△ADC 和△AEB 中,
因为AC = AB, AD = AE, CD = BE, 所以△ADC ≌ △AEB(SSS) .
八.局部当整体
例8 如图, 已知AB = AC, ∠B = ∠C , BD = CE, 试说明△ABE 与△ACD 全等的理由.

错解: 在△ABE 和△ACD 中,
因为AB = AC, ∠B = ∠C, BD = CE, 所以△ABE ≌ △ACD( SAS) .
错解分析: 错解没有认真地结合图形来分析条件, 错把三角形边上的一部分(BD 是BE 的一部分, CE 是CD 的一部分) 当成边来说明, 这不符合“边角边”条件.
正解: 因为BD = CE,
所以BD DE = CE DE,
即BE = CD.
在△ABE 和△ACD 中,
因为AB = AC, ∠B = ∠C, BE = CD,
所以△ABE ≌ △ACD( SAS) .
九.“同理可证”实际不同理
例9 已知: AD和A′D′分别是△ABC和△A′B′C′的中线,AB=A′B′,BC=B′C′,AD=A′D′.
求证:△ABC≌△A′B′C′.

错解: 如图,因为BD=BC, B′D ′=B′C′,BC=B′C′,
所以BD=B′D′. 在△ABD和△A′B′D′中, AB=A′B′,BD=B′D′,AD=A′D′,因此△ABD≌△A′B′D′.同理可证△ADC≌△A′D′C′.故△ABD △ADC≌△A′B′D′ △A′D′C′,即
△ABC≌△A′B′C′.
错解分析: 以上证法有两个错误:⑴用了不同理的同理可证.证明△ABD≌△A′B′D′与△ADC≌△A′D′C′的理由是不同的. 要证△ADC≌△A′D′C′,需证∠ADC=∠A′D′C′, 根据SAS来证; ⑵由两对全等三角形之和推出△ABC≌△A′B′C′,理由不充分.
正解: 由△ABD≌△A′B′D′,有∠B=∠B′. 在△ABC和△A′B′C′中, AB=A′B′,∠B=∠B′,BC=B′C′,因此△ABC≌△A ′B ′C′.
十.不顾条件任意引申
例10 已知:如图,AB=AC,BD=CE,AD=AE.
求证:BE=CD.

错解: 在△ABD和△ACE中,因为AB=AC,BD=CE,AD=AE,所以
△ABD≌△ACE,故∠1=∠2.于是∠DAC=∠BAE.故BE=CD.
错解分析:等角对等边成立的条件是在同一个三角形中.而这里∠DAC与∠BAE 虽然相等,但是,它们不在同一个三角形中,所以不能得出BE=CD.错解犯了不顾条件任意引申的错误.
正解:在△ABD和△ACE中,因为AB=AC,BD=CE,AD=AE,所以△ABD≌△ACE.故∠1=∠2.于是∠DAC=∠BAE.从而△ADC≌△AEB.故BE=DC.
,