如何分析财务数据老板才看得懂（学会分析毛利对财务BP来说到底有多重要）

据调查统计，2022年财务BP成为了众多财务人跳槽的首选岗位！

作为财务BP每天都要跟业务打交道，当财务对不同的产品（产品线）完成收入和成本核算后，就可以对相应的产品毛利进行分析了。

这几天受国际局势的影响，大宗商品原材料价格波动较大，增加了制造业的原料采购成本，成本上涨进而影响了产品的毛利。

毛利是企业净利润的基础，毛利率在一定程度上可以反映企业的竞争优势，如果企业具有持续性的竞争优势，它的毛利率会处在较高的水平，企业可以对其产品或服务自由定价，让售价远高于其产品或服务本身的成本；如果企业缺乏持续竞争的优势，它的毛利率就处在较低水平，企业就只能根据产品或服务的成本来定价，赚取微薄的利润。

我在群里看到有很多制造业的财务BP都在为分析毛利变动的原因而苦恼，今天我们的案例将结合Python教大家如何使用基期和当期的营业数据，快速分析毛利和毛利率变动的原因。

数据准备

获取实验数据，分为基期毛利数据和本期毛利数据：

import pandas as pd import warnings warnings.filterwarnings("ignore") pd.options.display.float_format = '{:,.2f}'.format file = '财会实验数据.xlsx' df0 = pd.read_excel(file, sheet_name='毛利基期数') df1 = pd.read_excel(file, sheet_name='毛利本期数') #df.fillna(0,inplace=True) df0

如何分析财务数据老板才看得懂（学会分析毛利对财务BP来说到底有多重要）(1)

计算指标

为基期数和本期数分别计算毛利、占比、单价、单位成本、成本率、毛利率等指标：

# a.创建计算函数 def margin(df): # 计算产品线汇总数，如果是字符串，填入文字‘合计’，数字的进行加总 df.loc['T'] = df.apply(lambda x: '合计' if isinstance(x.sum(),str) else x.sum()) df['毛利'] = df['收入']-df['成本'] df['占比'] = df['收入']/df.loc['T','收入'] df['单价'] = df['收入']/df['销量'] df['单位成本'] = df['成本']/df['销量'] df['成本率'] = df['成本']/df['收入'] df['毛利率'] = df['毛利']/df['收入']*100 # b.对基期数和本期数分别应用函数 margin(df0) margin(df1) df0

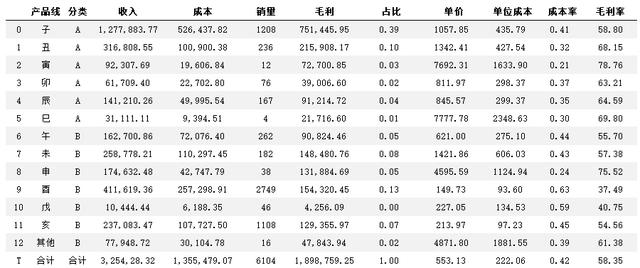
如何分析财务数据老板才看得懂（学会分析毛利对财务BP来说到底有多重要）(2)

数据处理

将两期数据进行拼接，注意suffixes参数填加同名字段不同表的后缀：

df2=df0.merge(df1,on=['产品线'，‘分类’]， how=‘outer’,suffixes=('2018','2019')) df2

如何分析财务数据老板才看得懂（学会分析毛利对财务BP来说到底有多重要）(3)

进行两期数据的分析比较

a.降价率 = 本期单价/基期单价-1

b.降本率 = 本期单位成本/基期单位成本-1

c.毛利差 = 本期毛利-基期毛利

df2['降价率']=df2['单价2019']/ df2['单价2018']-1 df2['降本率']=df2['单位成本2019']/ df2['单位成本2018']-1 df2['毛利差']=df2['毛利2019']/ df2['毛利2018'] df2['毛利率差']=df2['毛利率2019']- df2['毛利率2018'] #方便查看结果，缩短展示列 pd.concat([df2[产品线]， df2.loc[:,'降价率']]，axis=1)

如何分析财务数据老板才看得懂（学会分析毛利对财务BP来说到底有多重要）(4)

将毛利差拆分为价格影响、成本影响、销量影响:

d.价格对毛利的影响额 = (本期单价-基期单价)*本期销量

e.成本对毛利的影响额 = -(本期单位成本-基期单位成本)*本期销量

f.销量对毛利的影响额 = (本期销量-基期销量)*基期单位毛利

df2['价格影响'] = (df2['单价2019']-df2['单价2018'])*df2['销量2019'] df2['成本影响'] = -(df2['单位成本2019']-df2['单位成本2018'])*df2['销量2019'] df2['销量影响'] = (df2['销量2019']-df2['销量2018'])*(df2['单价2018']-df2['单位成本2018']) # 验证三个影响因素的合计等于毛利差 print(df2.iloc[:,-3:].sum(axis=1)-df2['毛利差']) #方便查看结果 pd.concat([df2['产品线'],df2.loc[:,'降价率':]],axis=1)

如何分析财务数据老板才看得懂（学会分析毛利对财务BP来说到底有多重要）(5)

将毛利率差拆分成价格和成本的影响（毛利与销量无关）：

g.成本影响毛利率 = 本期单位成本-基期单位成本/基期单价

h.价格影响毛利率 = -本期单位成本/本期单价本期单位成本/基期单价

i.除成本和价格单独对毛利的影响额外，即不同毛利的产品混合在一起所产生的影响

其中，g和h的分子分母同时乘本期销量，因为单个产品线的计算是否乘销量结果是一样的，但是产品线的合计如果用单位成本和单价计算就会失真，因此乘销量后的收入和成本总额进行计算。

df2['新收入'] = df2['单价2018']*df2['销量2019'] # 重算合计数，倒数4列的合计拿各产品线重新加总 df2.iloc[-1:,-4:] = df2.iloc[0:-1,-4:].sum().values df2['成本影响毛利率'] = df2['成本影响']/df2['新收入']*100 df2['价格影响毛利率'] = df2['毛利率2019']-(df2['新收入']-df2['成本2019'])/df2['新收入']*100 df2['混合影响毛利率'] = df2['毛利率差']-df2['成本影响毛利率']-df2['价格影响毛利率'] #方便查看结果 pd.concat([df2['产品线'],df2.loc[:,'降价率':]],axis=1)

如何分析财务数据老板才看得懂（学会分析毛利对财务BP来说到底有多重要）(6)

设计以上毛利分析模型的意义在于，如果数据有多维度，比如销售区域、大类、渠道等，可以将子类数据传入模型，分析每个子类的毛利：

# 如果要对源数据进行分类统计，可以将上述过程打包成一个大函数，将基期df和本期df作为参数传入，输出毛利影响分析表 def ma(df0,df1): margin(df0) margin(df1) # 将两期数据进行拼接 df2 = df0.merge(df1,on=['产品线','分类'],how='outer',suffixes=('2018', '2019')) # a.降价率 = 本期单价/基期单价-1 df2['降价率'] = df2['单价2019']/df2['单价2018']-1 # b.降本率 = 本期单位成本/基期单位成本-1 df2['降本率'] = df2['单位成本2019']/df2['单位成本2018']-1 # c.毛利差 = 本期毛利-基期毛利 df2['毛利差'] = df2['毛利2019']-df2['毛利2018'] df2['毛利率差'] = df2['毛利率2019']-df2['毛利率2018'] # d.价格对毛利的影响额 = (本期单价-基期单价)*本期销量 df2['价格影响'] = (df2['单价2019']-df2['单价2018'])*df2['销量2019'] # e.成本对毛利的影响额 = -(本期单位成本-基期单位成本)*本期销量 df2['成本影响'] = -(df2['单位成本2019']-df2['单位成本2018'])*df2['销量2019'] # f.销量对毛利的影响额 = (本期销量-基期销量)*基期单位毛利 df2['销量影响'] = (df2['销量2019']-df2['销量2018'])*(df2['单价2018']-df2['单位成本2018']) # 分析价格和成本对毛利率的影响（毛利与销量无关） df2['新收入'] = df2['单价2018']*df2['销量2019'] # 重算合计数 df2.iloc[-1:,-4:] = df2.iloc[0:-1,-4:].sum().values # 成本影响毛利率 = (本期单位成本-基期单位成本)/基期单价，分子分母同时乘本期销量 df2['成本影响毛利率'] = df2['成本影响']/df2['新收入']*100 # 价格影响毛利率 = -本期单位成本/本期单价本期单位成本/基期单价，分子分母同时乘本期销量 df2['价格影响毛利率'] = df2['毛利率2019']-(df2['新收入']-df2['成本2019'])/df2['新收入']*100 # 除成本和价格单独对毛利的影响额外，即不同毛利的产品混合在一起所产生的影响 df2['混合影响毛利率'] = df2['毛利率差']-df2['成本影响毛利率']- df2['价格影响毛利率'] return pd.concat([df2['产品线'], df2.loc[:,'降价率':]],axis=1) # 对A类产品进行分析，将过滤后的df作为参数传入ma函数 ma(df0.loc[df0['分类'] == 'A',:],df1.loc[df1['分类'] =='A',:])

如何分析财务数据老板才看得懂（学会分析毛利对财务BP来说到底有多重要）(7)