轻轻挤压桌子上的一张A4纸时,整个纸张在桌面上隆起形成波浪状(图1)。而卷起袖子或眨眼睛时,则会在袖子或眼睑上出现各种复杂褶皱。这类现象都可归纳为软薄膜在硬基底上受压产生的非线性失稳变形,在日常生活中无处不在。对于平面情况(零曲率),已经有学者对褶皱失稳现象进行了系统研究。然而,在更为复杂的曲面上,人们对其中的变形机理和起皱过程仍然知之甚少。
图1. 纸片在光滑桌面上受挤压的变形过程,可以看到单一的半波隆起直至两端接触。
今日,复旦大学青年研究员徐凡课题组发表于Physical Review Letters上的研究成果首次揭示了曲率影响下(圆柱核心)软薄膜在轴向受压时的非线性失稳演化全景(如图2)[1]。有趣的是,看似简单的现象背后却包含着复杂的非线性力学机理,即光滑(smooth)-褶皱(wrinkle)-凸脊(ridge)-松垂(sagging)的多重分岔失稳行为,是一个涉及多种模态连续转变的强非线性问题。如图3所示,在某一个载荷下,系统可能存在多个平衡状态,且比当前状态能量更低,促使系统向更低能量的模态分岔。实验(图2)中首先观察到周期性的轴对称正弦形褶皱,然后演变到局部的“凸脊”形模态。受曲率影响,凸脊的高度存在极限,并不会像平面情形(图1)下半波的高度接近于整个薄片对折的尺度。在到达这个挠度极限后,凸脊由于对称性破缺倒向一边而发生偏转。
图2. 软膜在圆柱面上的几种失稳模态。(a) 撸起的袖子,(b) 实验装置示意图,(c)-(f) 实验中随载荷增加从光滑(smooth)依次出现正弦形(wrinkle),凸脊形(ridge),松垂形(sagging ridge)模态,(g)-(j) 是其分别对应的特征示意图。
图3. 多重分岔的树状示意图,如应变-势能或载荷-位移的多重后屈曲分岔路径。每条分岔支路(不同颜色区别)对应一种失稳模态,多重分岔将导致模态选择与转化。
研究人员通过数值计算来定量预测这一演化过程(图4)。当轴向压缩载荷到达临界点时,圆柱核心上的光滑薄膜会屈曲失稳为正弦形模态,通过Koiter屈曲理论[2]可以预测其临界状态的应变及波长(接触对于屈曲并无显著影响)。而理论预测也表明,当曲率半径无穷大时(接近平面),结构整体变形为一个半波(图1)。随着载荷的增加(图4),正弦形褶皱的幅值随之增加,直到第二个临界点:其中一个波的幅值快速的增长,伴随着其余波的幅值剧减,形成局部凸脊形模态。凸脊的高度受几何尺寸(柱壳的半径和厚度)的影响,而与壳体的长度无关。当凸脊达到上限之后发生第三次分岔,凸脊偏转的同时会把周围区域的压应力释放。值得注意的是,采用不同的材料本构模型并不会对这一过程产生较大影响,说明该现象依赖于几何非线性而不是材料性质(如不同材质的衣服均会出现类似的褶皱形貌)。
图4. 后屈曲分岔演化相图。红线为凸脊顶峰的径向位移,蓝线表示与凸脊相邻的波峰位移。
研究人员进一步考察了加载与卸载过程。系统失稳产生的首个正弦形褶皱模态属于稳定的超临界分岔(supercritical bifurcation),而后两次分岔(正弦/凸脊,凸脊/松垂)属于不稳定的亚临界分岔(subcritical bifurcation),在正弦/凸脊和凸脊/松垂的转变区域产生迟滞现象(hysteresis)。通过比较加载/卸载两个阶段的能量差,发现在正弦/凸脊和凸脊/松垂两个过渡区域中,分别存在一个Maxwell应变。该应变表示处于过渡中的两种状态能量相等,可用于判断和预测后屈曲过程中相邻失稳模态的转变趋势。
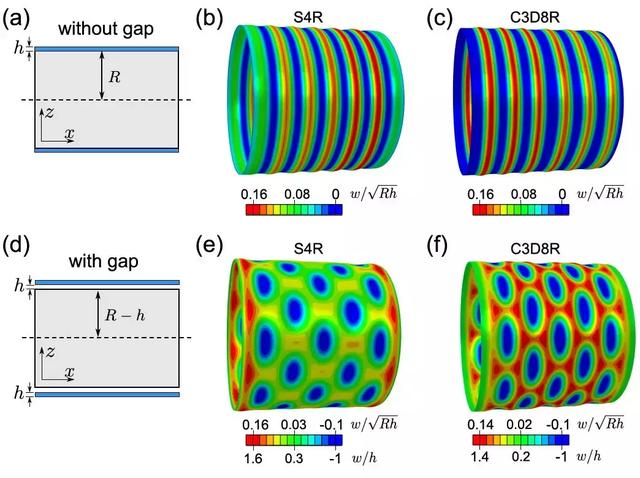
图5. 柱壳与核心的间隙可以影响并调控柱壳失稳模态的选择。
该研究也为上世纪60年代Horton[3],Almroth[4]等人研究单轴受压下金属薄壳屈曲的模态选择提供了一个科学的解释。当在柱壳中放入一个核心,且核心与柱壳的间隙与壳的厚度相当(以避免柱壳局部变形过大),则由于间隙产生的缺陷敏感性使屈曲时产生非轴对称的“钻石形”模态(diamond-like pattern) [5]。较大的间隙使壳体在屈曲后与核心接触,而较小甚至为零的间隙在结构屈曲前就已发生接触,易产生稳定的正弦形轴对称变形。研究发现可以通过控制孔隙的大小来进行失稳模态的调节与选择(轴对称/钻石形模态转变)。该发现也为软薄膜表面形貌的力学调控与设计提供了新的思路。
该文的第一作者为复旦大学航空航天系本科生杨易凡,通讯作者为复旦大学航空航天系青年研究员、博士生导师徐凡,曾获美国机械工程师学会法国分部青年研究员奖(ASME Prize, French section)。参与该研究的合作者还有香港城市大学数学系的戴晖辉教授和法国洛林大学国家科学研究中心(CNRS)的Michel Potier-Ferry教授。此研究受到国家自然科学基金(11602058, 11772094),上海市“晨光计划”(16CG01),香港GRF基金(11302417),以及法国国家科学研究基金(ANR-11-LABX-0008-01)等项目的资助。
参考文献
[1] Y. Yang, H.H. Dai, F. Xu, M. Potier-Ferry. Pattern transitionsin a soft cylindrical shell. Phys. Rev.Lett., accepted.
[2] A.M.A. van der Heijden, 2009. W.T. Koiter's Elastic Stability of Solids and Structures. CambridgeUniversity Press, New York.
[3] B.O. Almroth, A.M.C. Holmes, D.O. Brush, 1964. An experimentalstudy of the buckling of cylinders under axial compression. Exp. Mech. 4, 263-270.
[4] W.H. Horton, S.C. Durham, 1965. Imperfections, a maincontributor to scatter in experimental values of buckling load. Int. J. Solids Struct. 1, 59-72.
[5] F. Xu, M. Potier-Ferry, 2016. On axisymmetric/diamond-like modetransitions in axially compressed core-shell cylinders. J. Mech. Phys. Solids 94, 68-87.
,