线段型最值问题是历年中考命题的热点,常在压轴题中出现,由于此类问题都是变化过程中,图形大小或形状是随动点的运动而变化的,学生很难把握变化图形的形状及其大小,故大多数学生遇到最值是"谈虎色变"不敢下手或无从下手,本文拟通过实例分析,一起探讨线段型最值问题的三种解题策略。

利器一:化斜线为垂线,利用垂线段最短求解
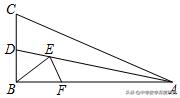
1.(2019秋•南丹县期中)如图,在Rt△ABC中,∠ABC=90°,AB=6,∠BAC=30°,∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE EF的最小值是_____.
【解析】:方法一:如图1所示,在AC边上截取AB′=AB,作B′F⊥AB于点F,交AD于点E,

∵AD平分∠BAC,∴∠BAE=∠B′AE,AE=AE,∴△ABE≌△AB′E(SAS).
∴BE=B′E,∴B′F=B′E EF=BE EF,
∵垂线段最短,∴此时BE EF最短.
∵AB=AB′=6,∠BAC=30°,∴B′F=1/2AB′=3.故答案为3.
方法二:如图2所示,在AC边上截取AG=AF,连接BG交AD于点E,作BH⊥AC于点H,

同方法一:得△AEG≌△AFG(SAS),∴EG=EF,∴BG=BE EG=BE EF,
当BG垂直于AC时最短,即BH的长最短,
∵AB=6,∠BAC=30°,∴BH=3.故答案为3.
2.(2020•新抚区二模)如图,边长为5的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是_______.

【解析】取CB的中点G,连接MG,根据等边三角形的性质可得BD=BG,再求出∠HBN=∠MBG,根据旋转的性质可得MB=NB,然后利用"边角边"证明∴△MBG≌△NBH,再根据全等三角形对应边相等可得HN=MG,然后根据垂线段最短,MG⊥CH时,MG最短,即HN最短,
此时∵∠BCH=1/2×60°=30°,CG=1/2AB=1/2×5=2.5,
∴MG=1/2CM=1/2×2.5=1.25,∴HN=1.25,故答案为:1.25.

3.(2020•新抚区二模)在△ABC中,∠ACB=45°,BC=5,AC=2√2,D是BC边上的动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接EC.
(1)如图a,求证:CE⊥BC;
(2)连接ED,M为AC的中点,N为ED的中点,连接MN,如图b.
①写出DE、AC,MN三条线段的数量关系,并说明理由;
②在点D运动的过程中,当BD的长为何值时,M,E两点之间的距离最小?最小值是_____,请直接写出结果.

【解析】(1)如图a,过点A作AH⊥AC交BC于H,由"SAS"可证△HAD≌△CAE,可得∠ACE=∠AHD=45°,可得结论;
(2)①如图b,连接AN,CN,由直角三角形的性质和等腰三角形的性质可得AN=CN=DN=EN=1/2DE,MN⊥AC,AM=CM=1/2AC,由勾股定理可得结论, MN² 1/4AC²=1/4DE²;
②根据垂线段最短即可解决问题.如图c中,

由(1)可知∠ECB=90°,∴CE⊥BC,
∴当ME⊥EC时,ME的值最小,
在Rt△ABC中,∵AH=AC=2√2,∴HC=4,
∵AM=MC=√2,
在Rt△CME中,∵∠ECM=∠CME=45°,
∴EC=EM=1,由(1)可知:△HAD≌△CAE,∴HD=EC=1,
∴CD=4﹣1=3,
∴BD=5﹣3=2,∴当BD=2时,EM的值最小,最小值为1。
方法归纳:
1、由上述例题可以发现"斜大于直"问题考察题型较为广泛,可以是单一线段最值,也可以是多条线段最值,还能是含系数的线段和的最值问题,无论是哪一种题型,都可以利用转化思想对问题进行巧妙处理。
1)单线段的最值常见于直线型的点到直线的距离,利用"隐点"和"隐线"加大题目难度
2)多线段和的最值始终遵循"同化异,折化直"的解题思路,如遇线段系数,通过三角函数进行转化
2、始终抓住"斜大于直"进行解题

利器二:利用将军饮马模型,化折线为直线
4.(2019秋•恩施市期末)如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD DE的最小值是______.

【解析】:作BF⊥AC于点F,如图所示,
∵在△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,∠BFA=90°,∴∠BAC=30°,∴AB=2BF,∴BF=8,
∵AM平分∠BAC,点D、E分别为AM、AB的动点,F
∴BD DE的最小值是BF,∴BD DE=8,故答案为:8.
5.(2019秋•平谷区期末)如图,△ABC是等边三角形,AB=2,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,则PE PC的最小值为( )
A.1 B.2 C.√3 D.2√3

【解析】根据等边三角形的三线合一的性质,连接BE交AD于点P,此时PB=PC,即可得到PE PC的最小值即为BE的长.如图,连接BE交AD于点P′,
∵,△ABC是等边三角形,AB=2,AD是BC边上的高,E是AC的中点,
∴AD、BE分别是等边三角形ABC边BC、AC的垂直平分线,
∴P′B=P′C,P′E P′C=P′E P′B=BE,根据两点之间线段最短,点P在点P′时,PE PC有最小值,最小值即为BE的长.利用勾股定理可求得BE=√3,所以P′E P′C的最小值为√3.故选:C.
6.(2019秋•碑林区校级月考)如图,在四边形ABCD中,∠BAD=90°,AB=AD.连接AC,若AC=5√2,则CD CB的最小值为_____.

【解析】根据旋转的性质将三角形ADC绕点A旋转90度到三角形ABE,使DC和BC在一条直线上,根据等腰直角三角形的性质即可求解.如图

易得△ABE≌△ADC,∴AE=AC=5√2,BE=DC,∠EAB=∠CAD,
∴∠EAC=∠BAD=90°,∴利用勾股定理可求得EC=10,∴CD CB=CB BE=EC=10.

7.(2018秋•碑林区期末)如图,在四边形ABCD中,∠B=∠D=90°,AB=BC,∠DAC=30°,AC=2,设Q,R分别是AB、AD上的动点,则△CQR的周长最小值是______.

【解析】:如图所示:

分别作点C关于AB、AD的对称点E、F,连接EF与AB、AD交于点Q、R,
此时△CQR的周长最小.根据对称性得:CR=ER,CQ=FQ,∴CR CQ QR=ER FQ QR=EF,∴△CQR的周长即为EF的长.
在Rt△ADC中,∵∠DAC=30°,AC=2,∴CD=1,
∵∠ABC=90°,AB=BC∴∠BAC=∠BCA=45°,∴BC=AC•sin45°=√2,
∵∠ADC=∠ABC=90°,∴A、B、C、D四点共圆,∴∠CDB=∠CAB=45°,
∠CBD=∠CAD=30°,在△CBD中,作CH⊥DB于H,

8.(2019秋•黄石港区校级期中)如图,∠AOB=20°,点M,N分别是边OA,OB上的定点,点P,Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP PQ QN最小时,则β﹣α的值为______.

【解析】:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP PQ QN最小,
∴∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∴∠QPN=1/2(180°﹣α)=∠AOB ∠MQP=20° 1/2(180°﹣β),
∴180°﹣α=40° (180°﹣β),∴β﹣α=40°.
方法归纳:求有关折线最小问题,通常情况下都是将折线问题化为直线,利用"两点之间线段最短"进行求解。

利器三:借助方程或函数知识,化几何为代数


方法归纳:将斜线转化成直线,或将折线转化成直线,通常要用几何变换,需要学生有比较敏锐的眼光,一般学生很难想到,这时不妨将几何问题代数化,将其转化成函数的最值问题或一元二次方程根的存在性问题。

在解决有关线段和的最小值和最大值的问题的时候,我们采用的数学思想方法是“化折为直”,有时需要通过对称变换作转化,然后根据“两点之间线段最短”这个知识来解决问题,这是将军饮马类问题的解题思想,将军饮马类问题根据定点个数和动点个数可以分为以下几类:一动点两定点(将军饮马原型),一定点两动点,两定点两动点,其中包括两动点之间距离不变的问题,我们称之为沿河饮马问题,统统这些问题的解题策略都是:作轴对称变换,然后化折为直,利用两点之间线段最短来解决问题。
,




