麦克斯韦-玻尔兹曼分布是描述一定温度下,理想气体分子运动速度的概率分布。宏观物理系统的温度,微观上来讲就是大量分子热运动的剧烈程度。单个气体分子的热运动有一个速度范围,通过与其它分子的碰撞而不断变化。然而对于大量气体分子来说,处于特定的速度范围的分子所占的比例基本不变。

麦克斯韦-玻尔兹曼分布就是理想气体分子的速度关于系统温度的函数:
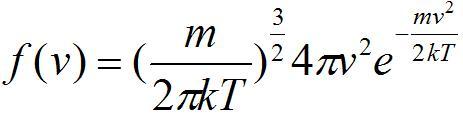
在这之前,首先了解什么是理想气体,以及系统的玻尔兹曼分布。
气体三定律:1、一定质量的气体,在等温过程中,压强跟体积成反比。即P1V1=P2V2=C1。
2、一定质量的气体,在压强不变时,体积与温度成正比。即V1/T1=V2/T2=C2。
3、一定质量的气体,当体积一定时,压强与温度成正比。即 P1/T1=P2/T2=C3。
综合气体三定律可得PV/T=C,C表示常量。
理想气体:在任何情况下都遵守气体三定律,服从方程PV/T=C的气体称为理想气体。其有三大性质:
1、理想气体分子之间没有相互作用力,即没有分子势能。
2、理想气体分子的碰撞不造成动能损失。
3、理想气体的内能是气体分子动能之和。

玻尔兹曼分布是系统中的粒子在各种可能的能量状态下的概率分布:
F∝e^(-ε/kT)
ε表示某个能量态的能量。
其概率密度分布为:
Pi=(e^-ε/kT)/∑(e^-εi/kT)
其中Pi是能量态i的概率,εi是量子态i的能量,k是玻尔兹曼常数,T是热力学温度,∑是对系统各个能量态概率的求和。
Pi=Ni/N
其中Ni为处于i能量态的粒子数,N为系统中的粒子总数。

麦克斯韦-玻尔兹曼分布也是一种玻尔兹曼分布,对于理想气体,能量是分子动能之和。气体分子的动能表示为:
E=mV²/2
m是单个分子的质量,V是分子速度矢量(Vx,Vy,Vz)。
将其代入玻尔兹曼分布:
Ni/N=(e^-ε/kT)/∑(e^-εi/kT)
=(e^-mV²/2kT)/∑(e^-mVi²/2kT)
根据Ni/N的分布与具有这些速度的气体分子的概率密度函数f(V)成正比,可知:
f(V)=C*(e^-mV²/2kT)/∑(e^-mVi²/2kT)
C是归一化常数,因为分子具有各种速度的概率必须为1,即上式在速度矢量V上的积分等于1,于是:
C=∑(e^-mVi²/2kT)/(m/2πkT)^(3/2)
代入f(V)可得:
f(V)=(m/2πkT)^(3/2)*e^(-mV²/2kT)

速度的麦克斯韦- 玻尔兹曼分布可以立即从速度矢量的分布得到,考虑到速度矢量是三维的,可得:
v=√( Vx² Vy² Vz²)
积分元是:dVxdVydVz
球坐标下的体积单位是:
dVxdVydVz=v²sinθdrdθdφ=v²dvdΩ
因为全空间立体角的积分值为4π,可知:
v²dv ∫dΩ=4πv²dv
最后通过对概率密度函数f(V)积分可得到速度的麦克斯韦- 玻尔兹曼概率分布:
f(v)=(m/2πkT)^(3/2)*4πv²*e^(-mv²/2kT)

麦克斯韦-玻尔兹曼分布是分子运动论的基础,诠释了压强和扩散等许多基本的气体性质。对于理想气体分子而言,粒子之间没有相互作用,量子效应可以忽略,因此麦克斯韦-玻尔兹曼分布提供了非常好的近似。但是当粒子的量子波长与粒子间距之比不够小时,量子效应不可忽略,则该分布就不再适用,这时就涉及到费米-狄拉克分布和玻色-爱因斯坦分布,进入了真正的量子分布领域。
,




