高职单招一直是中职生升入理想大学最重要的途径之一,还不了解的单招这个宝藏升学方式的同学快戳链接
此前,2022年四川省
高职单招报名及考试时间确定
2022年高职单招时间
报名时间 3月10日9:00至17日12:00
确认时间 3月19日9:00至23日12:00
考试时间 4月2日
此前,已经为大家带来了
语文的真题解析↓↓
单招真题解析【语文篇】那么今天就继续为大家带来单招数学·中职篇的真题解析吧
数学
根据2020年的真题分析,试卷主要分为三个大题:
一、单项选择题(10题,每小题5分,共50分)
二、填空题(3题,每小题4分,共12分)
三、解答题(3题,第14小题12分,第15、16小题各13分,共38分)
单项选择题
第一大题由10道选择题组成,考察了函数、集合、指数函数与对数函数、不等式、数列、概率、三角函数等。


考点汇总
函数
函数问题在单招考试中是重点和难点,在填空、选择、解答题中都会出现,最近几年解答题中必考。想在单招考试中得高分,把函数部分考好是关键。那么,如何复习函数呢?首先我们要注意定义域优先的原则。具体做到以下几点:
(1)函数是一种特殊的单值对应 f : A→B ,必须满足 A ,B 都是非空数集。其中 A 是定义域,而值域是 B 的子集。
(2)函数三要素最主要的是定义域和对应关系,当且仅当定义域和对应关系都相同时,才是相同的函数。
(3)根据所具备的条件,求其解析式,就是要求出对应关系。首先是要求出函数的定义域。求函数解析式的方法有直接法、待定系数法、换元法等。
(4)求函数的方法有配方法、換元法、基本不等式法、函数单调性法、数形结合法等。
(5)判断函数奇偶性,必先检测其定义域是否关于原点对称。
(6)求函数的值域和最值时,不但要重视对应关系的作用,还要优先考虑其定义域。
集合
集合是每次单招考试的必考内容。本考点概念性强,考题一般以选择题形式出现,难度不大。要把握元素与集合,集合与集合之间的关系。弄清楚有关的术语和符号,特别要把集合中元素的属性分析清楚,该知识点为送分题。大家平时复习时把握几个集合符号并能理解符号的意思就可以。
指数函数与对数函数
考察内容:
(1)理解有理数指数幂的概念。
(2)掌握实数指数幂及其运算法则。
(3)了解几种常见幂函数的图像和性质。
(4)理解指数函数的概念、图像和性质。
(5)理解对数的概念。
(6)了解积、商、幂的对数。
(7)了解对数函数的图像和性质。
(8)了解对数函数与对数函数的实际应用。
不等式
这个知识点在单招考试中每年都会涉及到。考试难度不大,其中一元二次不等式及其解法是重点,同学们在复习的时候要注意。
数列
数列是每年单招考试中的重点,多以填空、选择题为主,每年一道计算题成为单招考试的标配。所以,大家在复习这章时不仅要记忆一些基本的公式,还得理解如何进行简单的推理。该考点每年涉及14分之多,请大家予以重视。
考点:
(1)根据数列的前 n 项寻找规律,归纳通项公式或写出其中某项。
(2)考查关于的关系。
(3)运用公式进行简单计算(填空)。
等差数列是一种特殊的数列。在历年单招考试中都设计此部分内容,是命题的热点。经常出现的知识点:
(1)对等差数列的定义的考查。要牢记从第二项开始,以及每一项与前一项的差是同一常数这两点。
(2)要证明一个数列是等差数列,我们可以从两个角度考虑。第一是从定义开始(单招考试大都从此角度出题),即证明:当 n≥2时,有( d 是常数)恒成立;第二是通过等差中项来解决,即证明 n≥2时,有恒成立。

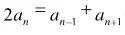
(3)有关计算问题。在等差数列中有5个量。只要知道其中3个量就可以求出其余的两个量,即“知三求二”。解题时选用公式要恰当,要善于减少运算量,达到快速准确的目的。

等比数列:等比数列是一种特殊的数列,也是单招考试中经常出现的知识点,考查题型以填空题、计算题为主。对等比数列定义的考查。重点是从第二项开始,以及每一项与其前一项比是同一常数这两点。要证明一个数列是等比数列,我们可以从两个角度进行,一是从定义角度,即证明:当 n≥2,时,有(q是常数)恒成立。二是应用等比中项来解决,即证明:当 n≥2时,有恒成立。
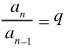

概率
考察内容:
(1)了解随机现象和概率的统计定义。
(2)理解必然事件和不可能事件的意义,了解基本事件的概念,理解随机事件的概率的性质。
(3)了解古典概率模型的含义,理解古典概率公式,并能运用它求出简单随机事件的概率。
(4)了解互不相容事件的加法定理和相互事件概率的乘法原理,并能用这些定理解决一些简单问题。
三角函数
(1)主要有三类求值问题:
①“给角求值”:一般所给出的角都是非特殊角,从表面来看求值是很难的,但仔细观察后会发现非特殊角与特殊角总有一定关系。解题时,要利用观察得到的关系,结合公式转化为特殊角并且消除非特殊角的三角函数而得解。
②“给值求值”:给出某些角的三角函数式的值,求另外些三角函数值。解题关键在于“变角”,使其角相同或具有某种关系。
③“给值求角”:实际是转化为“给值求值”,关键也是变角,把所求角用含己知角的式子表示,由所得的函数值结合该函数的单调区间求角。
(2)三角恒等变换的常用方法、技巧和原则:
①在化简求值和证明时常用如下方法:切化弦法、升幂降幂法、辅助元素法、以及“1”的代换法等。
②常用的拆角、拼角技巧如:

③化简为繁:变复角为单角,变不同角为同角,化非同名函数为同名函数,化高次为低次,化多项式为单项式,化无理式为有理式。
④消除差异:消除已知与未知,条件与结论,左端与右端,以及各项的次数、角、函数名称、结构等方面的差异。
(3)在解三角形中的三角变换问题时,“化简为繁”“化异为同”是解此类问题的突破口。
注意错选、多选或未选均无分。考试中遇到不会的题、拿捏不准的题,不要死磕,先跳过,完成了后面的题再回头思考。
参考答案:

填空题
第二大题由3道填空题组成,考察了数列、概率与统计、直线与圆等。
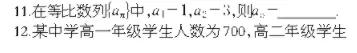

考点汇总
数列
数列是每年单招考试中的重点,多以填空、选择题为主,每年一道计算题成为单招考试的标配。所以,大家在复习这章时不仅要记忆一些基本的公式,还得理解如何进行简单的推理。该考点每年涉及14分之多,请大家予以重视。
考点:
(1)根据数列的前 n 项寻找规律,归纳通项公式或写出其中某项。
(2)考查关于的关系。

(3)运用公式进行简单计算(填空)。
等差数列是一种特殊的数列。在历年单招考试中都设计此部分内容,是命题的热点。经常出现的知识点:
(1)对等差数列的定义的考查。要牢记从第二项开始,以及每一项与前一项的差是同一常数这两点。
(2)要证明一个数列是等差数列,我们可以从两个角度考虑。第一是从定义开始(单招考试大都从此角度出题),即证明:当 n≥2时,有
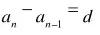
( d 是常数)恒成立;第二是通过等差中项来解决,即证明 n≥2时,有

恒成立。
(3)有关计算问题。在等差数列中有5个量

。只要知道其中3个量就可以求出其余的两个量,即“知三求二”。解题时选用公式要恰当,要善于减少运算量,达到快速准确的目的。
等比数列:等比数列是一种特殊的数列,也是单招考试中经常出现的知识点,考查题型以填空题、计算题为主。对等比数列定义的考查。重点是从第二项开始,以及每一项与其前一项比是同一常数这两点。要证明一个数列是等比数列,我们可以从两个角度进行,一是从定义角度,即证明:当 n≥2,时,有(q是常数)恒成立。二是应用等比中项来解决,即证明:当 n≥2时,有恒成立。


概率
考察内容:
(1)了解随机现象和概率的统计定义。
(2)理解必然事件和不可能事件的意义,了解基本事件的概念,理解随机事件的概率的性质。
(3)了解古典概率模型的含义,理解古典概率公式,并能运用它求出简单随机事件的概率。
(4)了解互不相容事件的加法定理和相互事件概率的乘法原理,并能用这些定理解决一些简单问题。
直线与圆
求切线方程时,若知道切点,则可直接利用公式。若过圆外一点求切线,则一般运用圆心到直线的距离等于半径来求,但注意有两点:一是解决与弦长有关的问题时,注意运用由半径、弦心距、弦长的一半构成的直角三角形;二是可以运用弦长公式。这就是通常所说的“几何法”“代数法”。判断两圆的位置关系时,应从圆心距和两圆半径的关系入手。
注意错填、不填均无分。
参考答案:

解答题
第三大题由3道解答题组成,考察了平面向量、立体几何、双曲线等。

考点汇总
平面向量
平面向量的基本概念及其线性运算是向量的基木知识。命题的落脚点以平面图形为载体考查考生对平面向量知识点的掌握程度。平面向量的基本概念是向量运算的基础,需要做到概念理解准确,方法运用恰当。
立体几何
考察内容:
(1)了解平面的概念、基本性质。
(2)理解直线与直线,直线与平面,平面与平面平行的判定与性质。
(3)了解直线与直线,直线与平面,平面与平面所成的角。
(4)了解柱、锥、球及其简单组合体的结构特征及面积、体积的计算。
双曲线
考察双曲线的标准方程和基本性质。
此部分着重考察考生思维灵活运用能力,有一定难度,小编建议,遇难题时,将前两大题基本完成以后,再回头来啃“硬骨头”。
注意解答应写出文字说明、证明过程或演算步骤。
参考答案:



小编提醒
数学是有难度的科目,考查考生的思维能力和灵活运用能力。但是考试中绝大部分题目都是基础题型,只要我们掌握科学的学习方法,不难取得令自己满意的分数。
,




