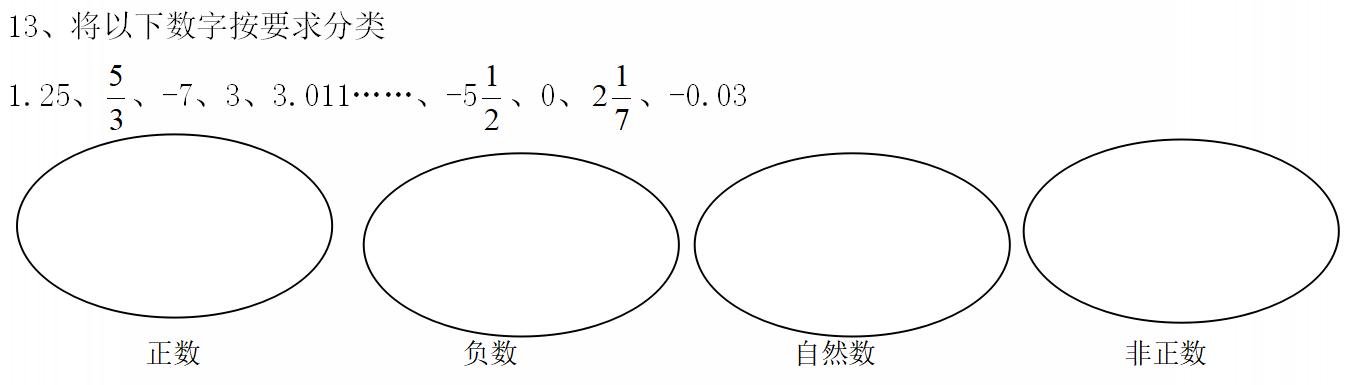
小学阶段在前面的学习中,已经认识了整数、小数和分数(小数也可归类在分数中)等,在六年级下学期,同学们会接触到一种新的数:负数。现在我们就来认识一下,什么是负数。
负数的产生人们在生活中经常会遇到各种相反意义的量。比如,在记账时有余有亏;在计算粮仓存米时,有时要记进粮食,有时要记出粮食。为了方便,人们就考虑了相反意义的数来表示。于是人们引入了正负数这个概念,把余钱进粮食记为正,把亏钱、出粮食记为负。可见正数和负数是生产实践中产生的。
我国三国时期的学者刘徽在建立负数的概念上有重大贡献。刘徽首先给出了正负数的定义,他说:“今两算得失相反,要令正负以名之。”意思是说,在计算过程中遇到具有相反意义的量,要用正数和负数来区分它们。
负数的定义1、以前所学的所有数(0除外)都是正数,也就是说正数前面的“ ”是可以省略不写的!
2、负数的定义:在正数前面加上“-”就是负数。
3、负数前面必定有“-”如果前面不是“-”(可能没有符号或者是“ ”)都是正数(0除外)。
4、0既不属于正数,也不属于负数,它是正数和负数的分界。
负数的作用1、负数是在人为规定正方向的前提下出现的。
2、负数常用来表示和正数意义相反的量。
3、在选择用正数还是负数表示时,首先看是否规定了正方向。
4、一般含有褒义的量用正数表示,含有贬义的量则用负数表示。
例:零上5°用 5℃表示;零下5°用-5℃表示。收入2000元用 2000元表示;支出500元用-500元表示。
常见负数的意义(1)地图上的负数:
中国地形图上,可以看到我国有一座世界最高峰—珠穆朗玛峰,图上标着8848,在西北部有一吐鲁番盆地,地图上标着-155米,你能说说8848米,-155米各表示什么吗?这两个高低是以谁为标准的?
(2)收入与支出
收入2600元( 2600元)
教育支出:300元 (-300元)
娱乐支出:500元 (-500元)。
(3)电梯间的负数
-3层表示地下三层,是以地面作为标准的。
(4)其他负数
以学校为起点,往东走为正,往西走位负,小明从学校走了 50m,又走了-100m,这时小明离学校的距离是50米。
食品包装上常注明:“净重500±5g,”表示食品的标准质量是500g,实际每袋最多不多于505g,最少不少于495g。
负数的读法和写法1、读法:在所读数的前面加上“负”
2、写法:在所写数的前面加上“-”
认识数轴

数轴
1、数轴的要素:正方向(箭头表示)、原点(0刻度)、单位长度(刻度)。
正方向:根据题意要求确定正方向,一般以向上或向右为正方向。
原点:也就是数字0所在的位置,一般根据表示数字的分布情况来确定,如果需要表示的正负数差不多相等时原点在数轴中间;如果正数比负数多得多原点偏左;如果负数比正数多得多原点偏右。
单位长度:由所要表示多的大小来决定刻度之间距离的大小,如果数字偏大刻度距离可以适当小一些,如果数字偏小刻度距离可以适当大一些。单位长度不一定每个刻度只能表示1。
2、用数轴表示数
在已给数轴上表示数:根据数字在对应的刻度上描点表示。
对于非整数的表示:将刻度进一步细分如,需要将0—1之间线段分为3等分则2等分处为该数。
对于负数的表示:负数都在0的左面,正数都在0的右面。例: 3.5在3和4中间,而-3.5在-3和-4中间。
3、根据数轴比较数的大小
所有的正数都大于负数;所有的负数都小于正数
0左边的数都是负数,0右边的数都是正数;
在数轴上越靠右边的数越大,越靠左边的数越小;
负数比较大小,不考虑负号,数字部分大的数反而小;
0大于所有的负数,小于所有的正数。 负数 < 0 < 正数
练习