(一)中世纪早期数学在欧洲的地位
为了传播基督的教义,教会开办了许多学校。在这些学校的课程里,数学内容尽管很少,但地位还是相当重要的。教会学校中的课程分为四科和三文。四科包括算术(纯粹数的科学)、音乐(数的应用)、几何(关于长度、面积、体积和其他诸量的学问)、天文(关于运动中的量的学问),三文包括修辞、逻辑和文法。
教会培养教士希望他们能通过说理捍卫神学和驳斥异端,而数学则被认为是训练神学说理的最好学科。教会提倡学习数学,还因为它对编制历法、预报节日大有用处。每个修道院中至少要有一个人能够作历法的计算。当然,数学在中世纪保持着它的生命力,另一个重要因素是占星术的需要。特别是中世纪后期,每个王宫都奉养着占星术士,他们帮助王公大人谋划政治决策、军事征战和个人事务。社会的需要,使得大学里也设有占星术的课程,占星术需要天文知识,必须懂得数学,故而占星术被看成是数学的一个分支。

数学显然不能在一个只信天国、向往来世的文明中繁荣生长。数学的创造需要一种自由的学术气氛,但是对中世纪的欧洲而言,现世生活的需要和经济发展的刺激则是鼓励人们投身数学的直接动力。1100年左右,新的变化开始了。欧洲人通过贸易和战争与阿拉伯人发生了直接接触。保存在伊斯兰世界的希腊著作被重新发现,王公贵族、教会领袖支持学者们去发掘这些学术宝藏。随着希腊著述的复活,欧洲人知道了欧几里得、阿基米德、阿波罗尼斯,甚至阿拉伯数学家阿尔·花拉子米的著作也被介绍到了欧洲。学术的复兴正好迎合了经济的繁荣,对数学的需要,使得欧洲人在计算技术、符号代数等新的数学知识上作出了自己的贡献。
(二)斐波那契
斐波那契(Leonardo Fibonacci,约1170—1250)生于比萨,父亲为商人,曾任海关总督。他随父亲到北非,幼年受教于伊斯兰学校。后来又在地中海沿岸旅行,留心各国数学。经过观察、比较,他认为阿拉伯国家的记数法及算术很好,于是在1202年写成《计算之书》(Liber Abaci)。此外他还写了《几何实践》(Practica Geometriae,1220)、《平方数书》(Liber Quadratorum,1225)、《花朵》(Flowers,1225)。
《计算之书》共15章。斐波那契在序言中说:“我把自己的一些方法和欧几里得几何学的技巧加进印度的方法中去,于是决定写成现在这本十五章的书,这样人们对这些东西不会再是那么生疏了。”所以,书中首先介绍印度—阿拉伯数码及其记数法,然后详细介绍了整数、分数、代数和一次同余式等。
意大利由于其特殊的地理位置而成为东西方文化交流的中转站,商贸往来促使人们需要熟练地掌握计算技能,所以斐波那契的书很快就传遍了欧洲,促进了欧洲数学的复兴。
《计算之书》中一个有趣的问题被称为“斐波那契的兔子”,即“假定大兔子每月生一对小兔,而小兔在两个月后长成大兔子,也开始生小兔子。那么问:自一对兔子开始,一年后可繁殖多少对兔子?”这个问题引出了著名的“斐波那契数列”:
1,1,2,3,5,8,13,21,34,……
它的构造特征是:自第3项开始,前面相邻两项的和就是后面一项。如1 1=2,2 3=5,3 5=8,……,13 21=34,等等。这个看起来不起眼的数列,却蕴含着非常深奥的数学知识。特别应当指出的是斐波那契数列与大自然的关系:
(1)斐波那契数列经常和花瓣的数目相合。
3……百合和蝴蝶花
5……金凤花、飞燕草
8……翠雀花
13……金盏草
21……紫菀
34,55,84……雏菊
(2)相继的斐波那契数的比越来越接近0.618034。例如,34/55=0.618182,55/89=0.617978,89/144=0.618056……这个数正是著名的黄金分割数。
(三)斯蒂文与十进小数
自1642年哥伦布发现美洲大陆以来,欧洲的商业蓬勃发展起来了。远洋航行需要精密的计算,商贸往来更需要便捷的数学,过去的笨拙方法越来越无法适应经济的发展了。因此,学者们想方设法改进复杂的计算方法,荷兰的斯蒂文(Simon Steven,1548—1620)就是其中的一个。
当时的荷兰还是西班牙的殖民地,荷兰人为摆脱殖民统治进行了长达40年的独立战争。斯蒂文是荷兰独立军中的一名主管会计。当时人们经常使用的利率是1/10、1/11、1/12……直到1/20,如果每次都个别计算,显然是非常麻烦的。斯蒂文为此而设计了一个利息表,为会计工作提供了极大的方便。
“有了利息表计算起来是方便多了,可是这么大的数字乘来除去还是很麻烦。麻烦出在哪里呢?”斯蒂文陷入了思考,发现利率为1/10的利息相对容易计算。于是,斯蒂文决定把利率的分母统一为10、100或1000。1584年,斯蒂文制定并出版了一个利率为1/10—5/100的利息表。
在十进分数的基础上,斯蒂文创造了十进小数的表示方法,他把①②③④⑤写在数字的上方或右边,表示整数后边的部分。如

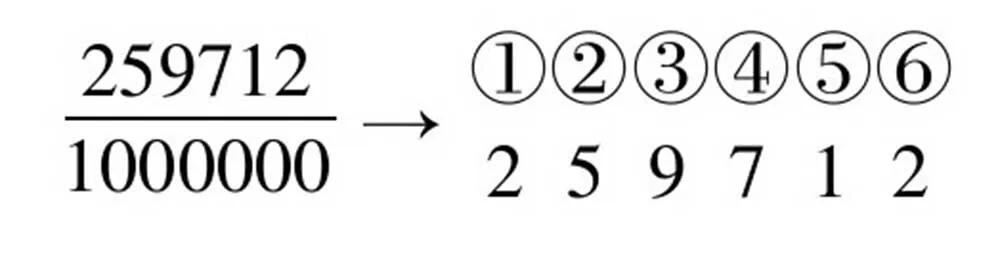
或


这种表示方法的好处是容易比较两个数字的大小,而且计算方法比分数计算还要方便。1585年,斯蒂文出版了《论十进算术》一书,这本书仅有6页,却是当时世界上第一本介绍小数及小数计算方法的书。斯蒂文的符号在今天看来也许有些笨拙,但其方法不久便获得普遍接受。在小册子的最后,斯蒂文还建议在度量衡及币制中也应用十进制,这些都在西方产生了深远的影响。
(四)纳皮尔与对数
文艺复兴时期在许多知识领域中,数值计算是非常重要的,例如,天文学、航海学、商业贸易、工程和军事,它们对计算速度和准确性的要求可以说与日俱增。在数学的历史上,这些增长的要求由于四项重要的发明而逐步得到满足。这四项发明是:印度—阿拉伯数码、十进小数、对数和计算机。现在我们要介绍第三个,即17世纪早期由纳皮尔(John Napier,1550—1617)完成的对数的发明。
纳皮尔出生于苏格兰的一个贵族家庭,在小时候就表现出引人注目的天才和丰富的想象力。比如,他预言将来会有许多威力强大的军事机械,而且还设计了它们的示意图:其中有一种枪炮,能清除方圆几公里内所有超过一英尺的高大动物;还有一种水下航行器;另有一种战车,它有“一张大嘴”,能“毁灭前进路上的任何东西”。在第一次世界大战期间,他的这些理想实现了:机关枪、潜水艇和坦克车。然而,真正引发数学计算的一场革命的,却是他对对数的发明。
请注意下面两行数列:


现在,我们计算16×64,可以在第一行找到它们相应的数4与6,计算4 6=10,10在第二行中对应的数1024就是我们要计算的乘积。对于除法,只要把“和”改为“差”。这种化“乘除”为“加减”的方法,正是纳皮尔对数的精髓。下面的对数公式是每位中学生都十分熟悉的:

而今天谁又能想到,在当时正是这一简单的性质,却“以其节省劳力而延长了天文学者的寿命!”(拉普拉斯)所以,对数发明后,不到一个世纪几乎传遍了世界,成为不可缺少的计算工具。伽利略甚至说:“给我空间、时间和对数,我即可创造一个宇宙!”
曾几何时,放在皮盒里挂在身上的对数计算尺,是大学校园里学习工程的学生的标志。而现在,袖珍计算器的普及,却使它们都被送进了博物馆。但是,对数的活力却依然未减。因为对数函数和指数函数的关系是分析学的关键部分。因此,它们在数学教育中占有重要的地位。这里顺便指出,现在对数普遍地被认为来源于指数。例如,如果n=bx,我们就说x是n的以b为底的对数。事实上,纳皮尔在创立对数概念的时候,并没有指数的概念。对数的建立先于指数,这是数学发展史上的一件趣闻。
(五)韦达与符号代数
数学符号对数学的发展所起的作用是不容置疑的。我们尽管无法对每一个数学符号的产生作出详细的历史考证,但是,一些重要的符号的出现,仍然在历史上留下了深深的印记。
在15世纪,人们最先使用的加和减的符号是p和m,这时德国商人用“ ”和“-”的记号表示重量的增加和差缺,很快地,“ ”“-”记号便为数学家们所采用。公元1481年之后,这些符号开始广泛出现在人们的手稿上。乘的符号“×”要归功于W.奥托(1574—1660),但当时遭到了反对,这个记号容易与字母X相混淆。等号“=”是雷科得(Robert Recorde,1510—1558)的创见:两条等长的平行线真是再相等不过了!
虽然用字母代替未知量,早在丢番图(Diophantus,约246—330)的时代就曾使用过,但一直没有形成一种共有的习惯。在16世纪,像radix(拉丁语“根”)、res(拉丁语“东西”)、cosa(意大利语“东西”)、coss(德语“东西”)这类词,都曾被用来作未知数。使得符号代数发生重要变革的是法国人韦达(F.Viete,1540—1603)。
韦达所受的专业训练是法律,可他把全部的业余时间都用于钻研数学。韦达潜心于卡丹(Jerome Cardan,1501—1576)、塔塔利亚(Tartaglia,原名Niccolo Fontana,1499—1557,塔塔利亚是绰号,意为口吃者)、斯蒂文和丢番图的著作,从而产生了使用字母表示数的想法。韦达不仅用字母表示未知量和未知量的乘幂,而且用字母来表示已知量。他把符号性代数称做“类的计算术”,而算术则是同数打交道的。这样,代数就脱离具体的数的束缚而抽象为研究一般的符号的形式和方程的学问。
韦达的著作以独特的形式包含了文艺复兴时期的全部数学内容。当然,精彩之处还是在代数方面,想想看,今天的中学生,有谁不熟悉一元二次方程的“韦达定理”呢?
(六)数学与科学革命
本节所介绍的印度—阿拉伯数码、十进小数、符号代数、对数等等,对于接受过高等数学教育的人来说,实在是再初等不过了。但是,我们决不可因此低估这些数学知识在推进科学进步的历史上发挥的重要作用。只有达到代数方法的熟练,才有可能为笛卡尔(René Descartes,1596—1650)创造解析几何作好必要的准备,而没有笛卡尔的解析几何,就根本不会有其后的牛顿与莱布尼兹(Gottfried Wilhelm Leibniz,1646—1716)的微积分,进而引力问题就决不会得到解决,整个牛顿体系就不会获得成功;也正是因为开普勒杰出的数学才能,才使得第谷丰富的观察材料真正变成推动天文学革命的关键因素。正如伽利略所说:“自然这部大书,是用数学语言写成的,它的字母是三角形、圆和各种几何图形。”
巴特菲尔德在他著名的《近代科学的起源》一书中曾这样写道:
……科学也给人以这样深刻的印象,即它们正在迫使数学站到整个时代的前沿。正如我们所知,没有数学家的种种成就,科学革命是绝不可能的。
,




