几何原本截图1
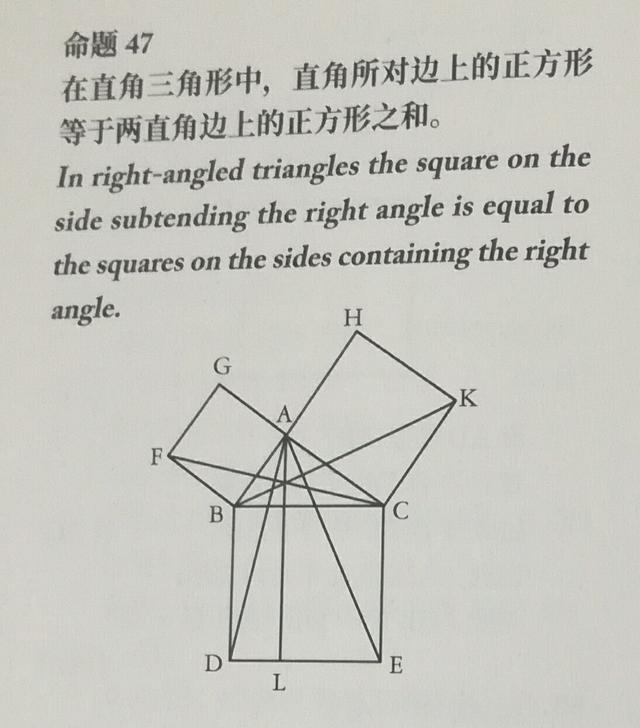
【命题47译文】命题47在直角三角形中,直角所对边上的正方形等于两直角边上的正方形之和。In right-angled triangles the square on the side subtending the right angle is equal to the squareson the sides containing the right angle.设ABC是直角三角形,角BAC是直角。
我说,BC上的正方形等于BA、AC上的正方形之和。
这是因为,在BC上作正方形BDEC,在BA、AC上作正方形GB、HC; [I. 46]
过A作AL平行于BD或CE,连接AD、FC。
于是,由于角BAC、BAG中的每一个都是直角,所以过直线BA上点A的两条直线AC、AG不在直线BA的同侧,且和直线BA所成邻角之和等于两直角,因此,CA和AG在同--直线上。 [I.14]同理,BA和AH也在同一-直线上。又,由于角DBC等于角FBA:因为每一个角都是直角:给它们分别加上角ABC;
因此,整个角DBA等于整个角FBC。
[公理2]
又,由于DB等于BC, FB等于BA,所以
两边AB、BD分别等于两边FB、BC;而角ABD等于角FBC;因此,底AD等于底FC,三角形ABD等于三角形FBC。 [I.4]
现在,平行四边形BL是三角形ABD的二倍,因为它们有同底BD且在相同的平行线BD、AL之间。[I.41]又,正方形GB是三角形FBC的二倍,因为它们也同底FB且在相同的平行线FB、GC之间。[I.41]<但等量的二倍也彼此相等。>
因此,平行四边形BL也等于正方形GB。
类似地,若连接AE、BK,则也可以证明平行四边形CL等于正方形HC;因此,整个正方形BDEC等于两个正方形GB、HC之和。 [公理2]
而正方形BDEC是在BC上作出的,正方形GB、HC是在BA、AC上作出的。因此,边BC上的正方形等于边BA、AC上的正方形之和。 这就是所要证明的。
欧几里得证明勾股定理的风车图
请看上图。图形由3个跳舞的正方形和5条辅助线组成,被称为欧几里得的风车。用这个风车图形,欧几里得漂亮地证明了勾股定理。
三角形ABC是直角三角形,3个正方形的边长分别是三角形的三条边。AL是垂线,将大正方形分为两个长方形。欧几里得的证法是围绕两个直角边上的正方形分别等于这两个长方形的面积展开的。
我们来看看这个出自欧几里得之手的漂亮的证明。
首先,欧几里得证明AGC三点共线。因为两个直角等于一个平角,而平角上的点都在一条直线上,所以很好证明。
同理可证ABH三点共线。这是事先埋下的伏笔,在后面的证明过程中会发挥作用。
接下来证明三角形ABD和三角形FBC全等。这也很好证明。两个三角形三条边和一个角相等,当然就全等。
开始就埋下的伏笔起作用了。现在我们知道了ACG和FB是平行线,ABH和CK也是平行线。根据平行线的性质,即两条平行线截取的垂线就是距离处处相等,容易证明等底等高三角形面积相等,等于等底等高的平行四边形面积的一半。
于是就证明了欧几里得定理:在一直角边上的正方形面积和一个长方形的面积相等,这长方形的一边是这直角边在斜边上的投影,另一边是斜边本身。
根据这个定理,正方形ABGF等于长方形BDL,正方形ACHK等于长方形CEL。
于是就证明了勾股定理。
欧几里得的这个证明和三国时期吴国数学家赵爽的证明分别代表了东西方数学的不同风格。
对于直角三角形还有一个有趣的定理是垂线定理:
在直角三角形中,以斜边上的垂线为边的正方形面积等于以斜边上两线段为边的长方形的面积。
解释一下:设垂线AL和BC交于点J,定理的意思是说AJ的平方等于BJ×JC。
也就是说BJ:AJ=AJ:JC,即AJ是比例中项。如果BJ和JC是两个数,那么AJ就是这两个数的几何平均数。

几何原本对勾股定理的逆定理的证明截图
【命题48译文】命题48在一个三角形中,若一边上的正方形等于三角形其余两边上的正方形之和,则其余两边所夹的角为直角。If in a triangle the square on one of the sides be equal to the squares on the remaining two sids
of the triangle, the angle contained by the remaining two sides of the triangle is right.在三角形ABC中,设边BC上的正方形等于边BA、AC上的正方形之和;我说,角BAC是直角。这是因为,从点A作AD与直线AC成直角,取AD等于BA,连接DC。由于DA等于AB,所以DA上的正方形也等于AB上的正方形。给它们分别加上AC上的正方形;因此,DA、AC上的正方形之和等于BA、AC上的正方形之和。但DC上的正方形等于DA、AC上的正方形之和,因为角DAC是直角; [I. 47]而BC上的正方形等于BA、AC上的正方形之和,因为这是假设;因此,DC上的正方形等于BC上的正方形,因此,边DC也等于边BC。又,由于DA等于AB, AC公用,所以两边DA、AC等于两边BA、AC;而底DC等于底BC;因此,角DAC等于角BAC。 [I. 8]但角DAC是直角;因此,角BAC也是直角。 这就是所要证明的。
《几何原本》的这两张截图来自2019年江西人民出版社出版的图书,作者是【古希腊】欧几里得。2019年江西人民出版社出版的图书,作者是【古希腊】欧几里得。
书 名:《几何原本》 ,又 名《原本》 ,原版名称:Στοιχεῖα ,译 者:张卜天
ISBN:9787210118046 ,共480页,定 价78 元。江西人民出版社 ,出版时间:2019-12-10
装 帧:平装 。开 本:16开
欧几里得,公元前330—公元前225,古希腊人,数学家。其著作《几何原本》是欧洲数学的基础,奠定了几何学、数学和科学的发展。对西方人的思维方法有深远的影响,被称为“几何之父”。
译 者简介:张卜天,男,1979年9月生。北京大学哲学系博士,现为清华大学人文学院科学史系长聘教授、中国社会科学院自然科学史研究所研究员。曾任英国剑桥李约瑟研究所访问学者,并曾于美国得克萨斯大学奥斯汀分校物理系就读,师从1979年的诺贝尔物理学奖得主史蒂文·温伯格。已有哲学和科学史相关译著五十余本。
最后说一句,我们课本里见到的勾股定理是代数形式,余弦定理也是代数形式,而《几何原本》里的勾股定理和余弦定理都是几何形式。
科学尚未普及,媒体还需努力。感谢阅读,再见。
,