开区间上的凸(包括上凸和下凸)函数不一定可导,但它是一定连续的。之所以提出这样的问题,是因为开区间上的凸函数还有一个非常重要的性质,那就是在开区间上任一点都存在左、右导数。
设f为开区间I内的凸(凹)函数,证明:f在I内任一点x0都存在左、右导数.
证:设f为开区间I内的凸(上凸)函数,取充分小的h2>h1>0,使x0±h2∈I,【自然也有x0±h1∈I】
则对x0-h2<x0-h1<x0<x0 h1<x0 h2,有
(f(x0 h1)-f(x0))/h1>=(f(x0 h2)-f(x0))/h2,(f(x0)-f(x0-h1))/h1<=(f(x0)-f(x0-h2))/h2,【上 凸 的曲线, 过同一点(x0,f(x0))的割线,另一个交点越靠右,割线的斜率越小】
令F(h)=(f(x0 h)-f(x0))/h, G(h)=(f(x0)-f(x0-h))/h, 则当h>0时,F为减函数,G为增函数. 【因为当0<h1<h2时,F(h1)>=F(h2),G(h1)<=G(h2)】
任取x’∈I且x’<x0,则对任何h>0,只要x0 h∈I,都有
(f(x0)-f(x’))/(x0-x')>=(f(x0 h)-f(x0))/h=F(h),即F(h)在h>0上有上界,
根据单调有界定理,可知lim(h->0 )F(h)=lim(h->0 )(f(x0 h)-f(x0))/h存在,即f在x0有右导数;
任取x”∈I且x”>x0,则对任何h<0,只要x0 h∈I,都有
(f(x0)-f(x”))/(x0-x”)<=(f(x0)-f(x0-h))/h=G(h),即G(h)在h>0上有下界,
所以lim(h->0 )G(h)=lim(h->0 )(f(x0)-f(x0-h))/h存在,即f在x0有左导数;【注意左 导数是有两个定义公式的,另一个是lim(h->0-)G(h)=lim(h->0-)(f(x0 h)-f(x0))/h,更加常用,但在这里用起来十分别扭】
若f(x)凹(下凸),则-f(x)凸,-f(x)在任一点x0存在左、右导数;从而f(x)在任何一点x0也存在左、右导数. 得证!
下面证明:开区间I上的凸(凹)函数不一定可导.
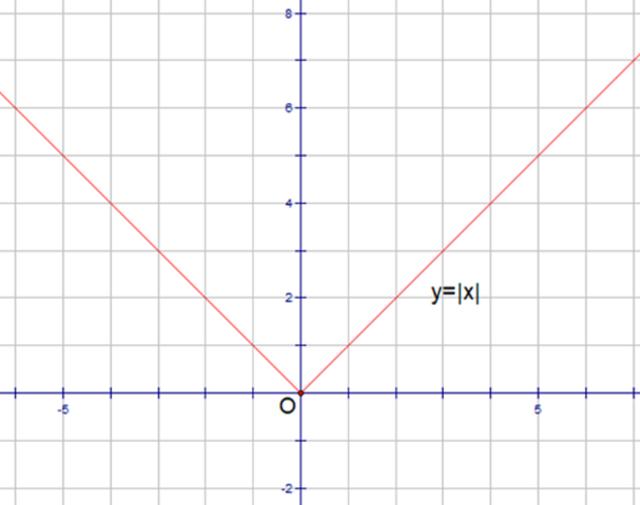
只需找到一个反例,如:f(x)=|x|是R上的凸函数,
它在R上任一点x0都存在左、右导数.
但在x=0,有f’ (0)=1, f’-(0)=-1,
f’ (0)≠f’-(0), f(x) 在 x=0不可导,
∴开区间I上的凸(凹函数)不一定可导.
虽然左右导数存在,不一定可导,但是左右导数存在,则足以说明函数是连续的。即开区间上的凸(凹)函数不一定可导,但一定连续。
,




