类型之三:整体代入
这种类型的特点是:代数式中字母的值不能或不用求出,对已知式和待求式作变形处理,使其含有共同的代数式,再用已知式中的部分去替换待求式中的部分,就可求得代数式的值。
例一
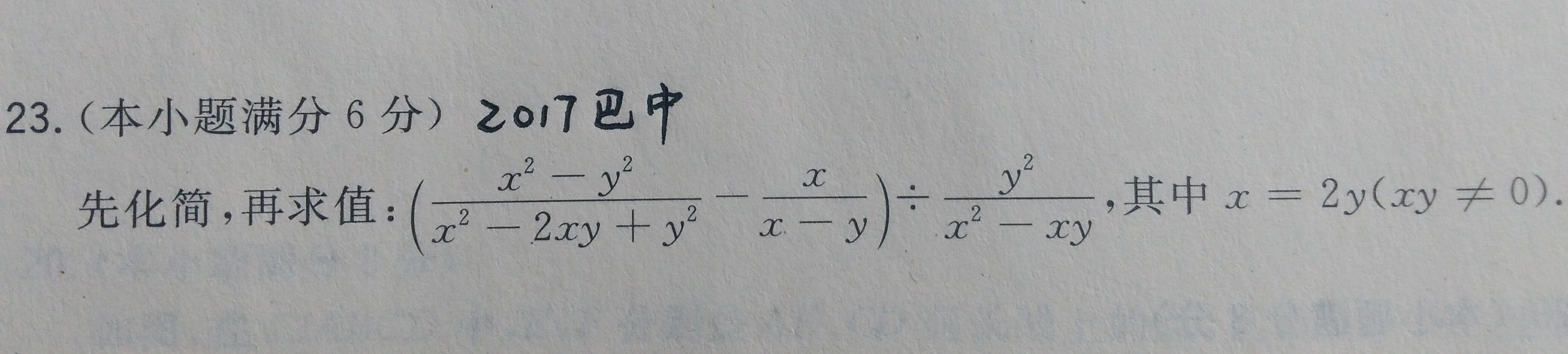
解析:
此题考查分式化简求值。“三傻大闹宝莱坞”,平方差公式、完全平方公式、提取公因式三班武艺齐上阵。可见出题人用心之良苦!边背公式边分解因式:x²--y²=(x y)·(x--y), x²--2xy y²=(x--y)², x²--xy=x·(x--y)。接下来注意分式减法及除法变乘法的运算。注意约分。x的取值显然不是具体数,当然要整体代入了。y可以约掉。出这个题的专家比较仁慈,2y就像个常数,叫我们直接代入求值。有时候整人的专家扔给你x--2y=0或(x--2y)²=0之类的玩意儿,你可要看得懂!
解答过程:

例二
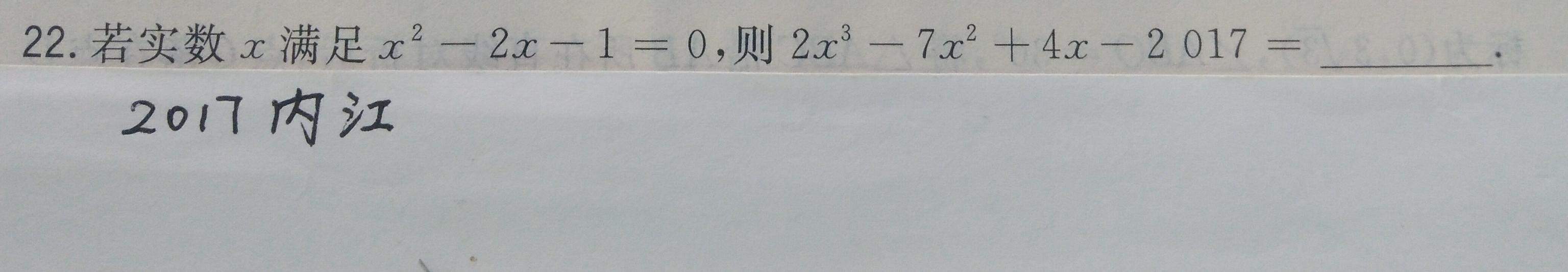
解析:
这道题中的待求式不需化简。学过一元二次方程解法 的学哥学姐们立刻就从那个方程中得知了x的取值,然后代入求值。但是x³的运算就让你烦。这边七八年级的学弟学妹们早已跃跃欲试,能不能整体代入呢?有的移项之后得到x²=2x 1,有的得到x²-2x=1,一步步代入替换,几番拆分、组合, 不断地降次,字母项全抵消了,都得到了-2020。第二个方法还优于第一个。整体代入求值的妙处可见一斑。
解答过程:
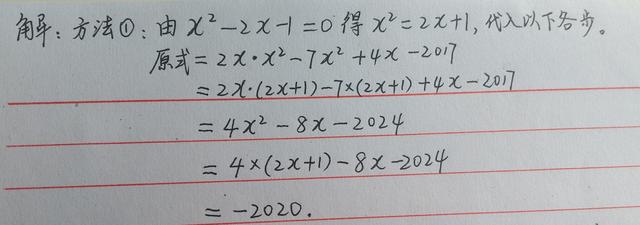

例三

解析:
这道题考查一元二次方程根与系数的关系,不需要解方程。让我们一起来回顾一下:设一元二次方程ax² bx c=0(a≠0)的两个根为x₁,x₂,则x₁ x₂=-b/a,x₁·x₂=c/a.另外还要熟练掌握几个恒等变形关系式:x₁² x₂²=(x₁ x₂)²-2x₁x₂,x₁² x₂²=(x₁-x₂)²+2x₁x₂,注意式中的符号。
解答过程:
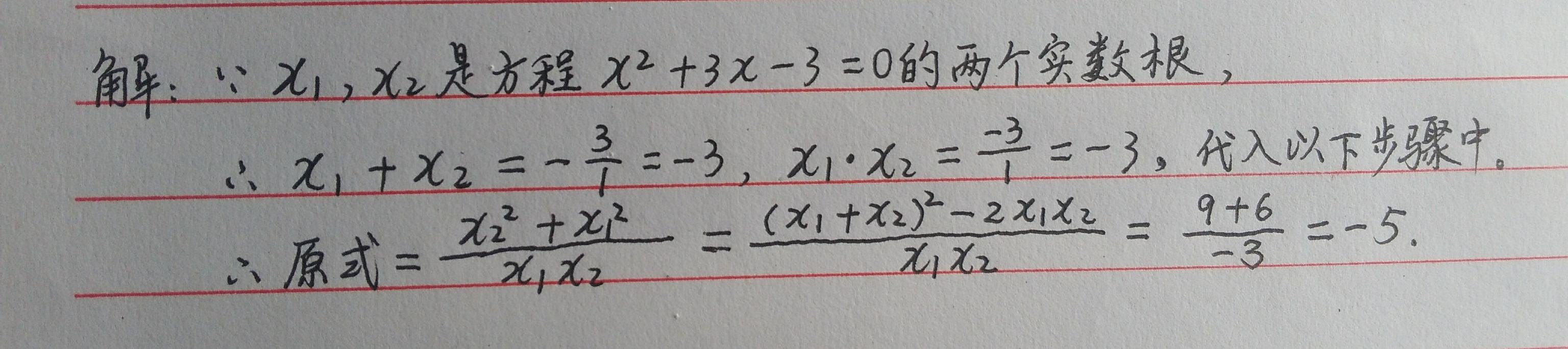
例四

解析:
这种题应由待求式想到(x 1/x)²或(x-1/x)²的形式(可通过配方达成),然后反观已知等式,一般通过将方程两边同时除以x,可得到(x 1/x)或(x-1/x)的形式,再做平方处理或整体代入。
解答过程:

最后欢迎你来挑战一个:






