一、实际问题与二元一次方程组的思路

1.列方程组解应用题的基本思想列方程组解应用题,是把“未知”转换成“已知”的重要方法,它的关键是把已知量和未知量联系起来,找出题目中的等量关系。
一般来说,有几个未知量就必须列出几个方程,所列方程必须满足:
① 方程两边表示的是同类量;
② 同类量的单位要统一;
③ 方程两边的数要相等。
2.列二元一次方程组解应用题的一般步骤设:
用两个字母表示问题中的两个未知数;
列:列出方程组(分析题意,找出两个等量关系,根据等量关系列出方程组);
解:解方程组,求出未知数的值;
答:写出答案。
3.要点诠释
(1)“设”、“答”两步,都要写清单位名称;
(2)一般来说,设几个未知数就应该列出几个方程并组成方程组。
二、八大典型例题详解
1.和差倍数问题
知识梳理和差问题是已知两个数的和或这两个数的差,以及这两个数之间的倍数关系,求这两个数各是多少。
典型例题:

【思路点拨】由甲乙两人2分钟共打了240个字可以得到第一个等量关系式2(x y)=240,再由甲每分钟比乙多打10个字可以得到第二个等量关系式x-y=10,组成方程组求解即可。
变式拓展:

【思路点拨】由甲组学生人数是乙组的3倍可以得到第一个等量关系式x=3y,由乙组的学生人数比甲组的3倍少40人可以得到第二个等量关系式3x-y=40,组成方程组求解即可。
2.产品配套问题
知识梳理总人数等于生产各个产品的人数之和;各个产品数量之间的比例符合整体要求。
典型例题:

【思路点拨】本题的第一个等量关系比较容易得出:生产螺钉和螺母的工人共有22名;第二个等量关系的得出要弄清螺钉与螺母是如何配套的,即螺母的数量是螺钉的数量的2倍(注意:别把2倍的关系写反)。
变式拓展:

【思路点拨】根据共有170名学生可得出第一个等量关系x y=170,根据每个树坑对应一棵树可得第二个等量关系3x=7y,组成方程组求解即可。
3.工作量问题
知识梳理我们在解决工程问题时通常把工作总量看成1;
工作量=工作效率×工作时间;
总工作量=每个个体工作量之和;
工作效率=工作量÷工作时间(即单位时间的工作量);
工作效率=1÷完成工作的总时间。
典型例题:

【思路点拨】

变式拓展:

【思路点拨】

4.利润问题
知识梳理商品利润=商品售价-商品进价;利润率=利润÷进价×100%。
典型例题:

【思路点拨】本题有两个未知数,即商品本钱和预售总价,也有两个明显的等量关系,即两种打折出售的获利情况,根据售价-成本-存货费用=利润,可以列出方程组求解即可。
变式拓展:

【思路点拨】本题易知第一个等量关系为甲乙两种商品共50件,则有x y=50。
根据甲乙商品的进价和利润率可知甲商品每件利润为35×0.2=7元,乙商品每件利润为20×0.15=3元,再由所获总利润得到第二个等量关系,组成方程组求解即可。
5.行程问题
知识梳理路程=速度×时间;
相遇问题:快行距+慢行距=原距追及问题:
快行距-慢行距=原距航行问题:
顺水(风)速度=静水(风)速度+水流(风)速度逆水(风)速度=静水(风)速度-水流(风)速度
典型例题:

【思路点拨】这两个问题均可以利用路程、速度和时间之间的关系列方程(组)求解,要明确快车与慢车的路程与A、B两地的距离之间的关系,相向而行两车相遇时:快车路程 慢车路程=A、B两地距离;同向而行两车相遇时:快车路程-慢车路程=A、B两地距离。
变式拓展:

【思路点拨】根据水流速度与船在静水中的速度的关系可以得到船的顺水速度和逆水速度,再根据路程=时间×速度列出方程组求解。
6.存贷款问题
知识梳理利息=本金×利率×期数;本息和(本利和)=本金+利息。
典型例题:

【思路点拨】本题的等量关系:甲种贷款 乙种贷款=13万元;甲种贷款的年利息 乙种贷款的年利息=6075元。
变式拓展:
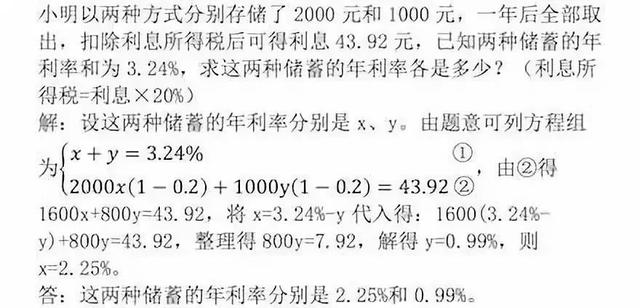
【思路点拨】本题两种储蓄的年利率之和为3.24%,由此可得到第一个等量关系x y=3.24%,再由两种储蓄的利息之和可得第二个等量关系,列方程组求解即可。
7.数字问题
知识梳理已知各数位上的数字,写出两位数,三位数等这类问题一般设间接未知数,例如:若一个两位数的个位数字为a,十位数字为b,则这个两位数可以表示为10b a。
典型例题:

【思路点拨】本题中的等量关系:
①个位上的数-十位上的数=5;
②原数 新数=143。
变式拓展:
【思路点拨】本题中的等量关系:
①个位上的数 十位上的数=8;
②原数-新数=18。
8.方案问题
知识梳理在解决实际问题时,需合理安排,从几种方案中,选择最佳方案。
要点诠释:方案选择的题目较长,有时方案不止一种,阅读时应抓住重点,比较几种方案得出最佳方案。
典型例题:

【思路点拨】(1)本小问两个等量关系均可利用货物的总吨数等于两种车型所运货物吨数之和,每种车型所运货物的吨数等于该种车的数量乘以每辆车装满货物时可运输的货物吨数,列出方程即可。
(2)根据货物的总吨数等于两种车型所运货物吨数之和列出方程,求解即可。
(3)总费用等于A型车的总费用加上B型车的总费用,比较三种方案的费用得出最省钱的租车方案。
变式拓展:






