前些日子,有位家长给我发信息说,她的孩子对这个乘法分配律还是不懂,问有没有这方面的题,她想让孩子在暑假里面做一做。其实,乘法分配律在所有的运算定律中,是个难点。在教学这部分内容的时候,孩子们出现的错误特别多,说到底,还是算理没搞明白。

了解“乘法分配律”得从解决问题入手。在此,我举了个简单的例题“一件上衣65元,一条裤子35元,买5件上衣和5条裤子,一共需要多少钱?”
先分析题意,已知上衣和裤子的单价,又知上衣和裤子各买5件(条),数量相等,其实也就是买5套衣服。要求的就是5套衣服的总价。
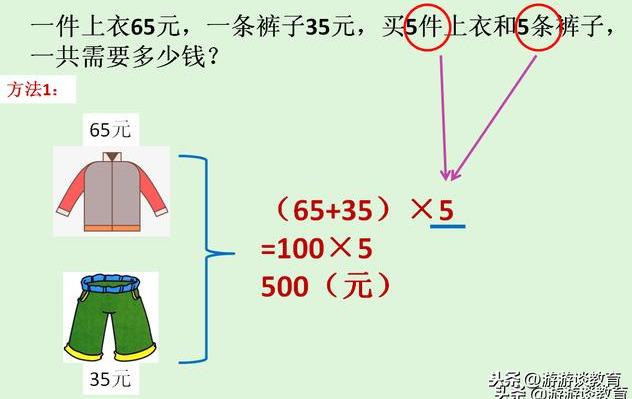
解决这个问题,有两种方法:一是先算出一件上衣和一条裤子一共需要多少钱(也就是先算一套衣服的价钱),然后再乘5(买了5套),两步就能算出总价,列成综合算式是:(65 35)×5=100×5=500(元);二是分别算出5件上衣的价钱,和5条裤子的价钱,再把两个钱数加起来,就是5套衣服的总价了,这个方法得用三步计算,列成综合算式是:65×5 35×5=325 175=500(元)。

由于这两种方法都是计算5件上衣和5条裤子的总价的,结果都是500元,所以,可以用等号把这两道综合算式连接起来,即:(65 35)×5=65×5 35×5。这其实就是乘法分配律的运算形式,如果用字母a表示上衣的价钱65元,用b表示裤子的价钱35元,用c表示购买的数量5,那么,上式就变成(a b)×c=a×c b×c。用文字表述,即:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫做乘法分配律。
这里,要注意“分别相乘”这几个字,结合例题,也就是上衣单价乘5,别忘了裤子单价也要乘5,才能算出完整的5套衣服的总价。通常孩子们容易错在只乘了一个5,总是忘记“分别相乘”四字。

在上述例题中,用字母表示还可以写成a×(b c)=a×b a×c,这里只是把字母换了一下位置而已,其中a表示为数量5,b和c分别表示成上衣和裤子的单价。在乘法分配律中,还有两种变形的运算公式(a-b)×c=a×c-b×c;a×(b - c)=a×b -a×c,就是把“ ”换成了“-”而已。

再举一个例题:一共有25个小组,每组里4人负责挖坑、种树,2人负责抬水、浇树。一共有多少名同学参加了这次植树活动?
这道题,同样也有两种解法:(4 2)×25=6×25=150(名) 和4×25 2×25=100 50=150(名)
比较上面两道例题,第一道用两个数的和与一个数相乘的方法来做比较简单:(65 35)×5=100×5=500(元),因为括号里的两个数可以凑成整百;而第二道用先把它们与这个数分别相乘,再相加的方法做简单一些:4×25 2×25=100 50=150(名),因为“4×25”和“2×25”在计算上比“6×25”更加好算。

因此,以后在做简便计算的题时,要具体情况具体分析,比如做乘法分配律的题,先观察,看看(a b)×c=a×c b×c,用左边这种方式好算,还是右边这种方式简单,然后再转化成最简便的方法来算。

总之,万变不离其宗,弄明白算理了,解决此类型的题就会迎刃而解。
,





