【教学内容】
人教版六年级下册第三单元《圆柱与圆锥》第27 页例 7。
一、复习旧知
师:请回忆并写出圆柱的体积公式。
预设:V=Sh
V=πr^ h
师:体积和容积有什么区别和联系?
预设 1:体积是求这个物体所占空间的大小。容积是求这个容器所能容纳物品的多少。
预设 2:体积和容积的算法一样(所用公式一样),但是有时单位有所不同。
预设 3:一般情况下容积都比体积小。
【设计意图:通过复习旧知为后面的学习起到铺垫的作用。便于学生很好地完成后面的任务。】
师:今天这节课,我们要继续探究和圆柱体积有关的实际问题。
(板书:问题解决——求瓶子的容积)
二、自学探究
投影题目:

师:请同学们自己阅读题目,在导学案自学探究中,找出题目中的数学信息,并用黑色的笔画出数学信息,用红色的笔画出数学问题。
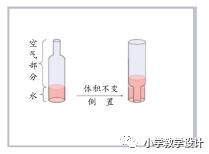
1. 出示信息和问题:一个内直径为 8 厘米的瓶子,无水部分的圆柱高度是 18cm,水的高度是 7 厘米,求瓶子的容积。
2.黑板上贴“阅读理解”,学生汇报信息,教师贴出教具瓶子。重点突出有水部分的圆柱贴片和倒置的无水贴片(双层)。
3.提出问题。
师:我们要求的是这个瓶子的容积,它能直接利用所学体积公式计算容积吗?你有什么想法?
【设计意图:找数学信息及问题的目的在于培养学生良好的数学学习习惯。巧做教具,贴出圆柱有水部分和倒置无水部分的贴片是为后续转化成新圆柱做铺垫。】
三、动手操作,验证猜想
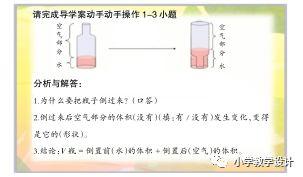
分析与解答:
1.贴“分析与解答”,小组讨论。
以小组为单位,拿出矿泉水,找一名同学喝掉一部分水,找出计算瓶子容积的方法,在小组内交流。
师:请以小组为单位,讨论一下你们打算用什么办法解决瓶子的容积问题。
2.交流反馈。
师:怎样求瓶子的容积?
(学生汇报)
师:为什么要把瓶子倒过来呢?
师:瓶子里的水喝多少合适?
师:倒置前后,瓶子的容积、空气的体积、水的
体积大小有没有发生变化?只是什么发生了变化?(形状)
师:谁能结合教具完整地再跟大家讲解一下如何求瓶子的容积?
【设计意图:问题串的形式,引发学生深入思考。并以小组为单位合作交流、主动探索,让学生亲身经历、体验分析问题和解决问题的过程,掌握、理解转化这一重要的数学思想及策略。】
预设:通过倒置,将瓶子的容积转化成两个小圆柱的体积——倒置前水的体积加上倒置后空气的体积,就可以解决问题了。
3. 梳理方法。
师:(电脑演示)瓶子的容积是由水的体积和空气的体积组成的,先求出水的体积后,再让瓶子倒置,把不规则空气体积转化成圆柱,求出它的体积。这样,只要把倒置前水的体积和倒置后空气的体积加起来就可以得到这个瓶子的容积了。
【设计意图:通过 PPT 动态演示,将抽象的问题形象化、复杂的问题明晰化、静态的问题动态化,让学生更直观地了解不规则的物体如何转化成了规则的物体。】
4.思考:每个组员喝了的水都不一样,那么求出来这个瓶子的容积是一样的吗?
预设 1:不一样。
预设 2:一样的,因为喝了的水越多,水的体积就会越少,喝了的水少了,水的体积就多了,不管怎么变,瓶子的容积是没有变化的,也就是总量不变。
【设计意图:让学生在实际事物中体会数学变中有不变的思想。】
5. 请完成导学案动手操作 1~3 小题。(点名汇报)
师:我把大家的方法记录下来:V 瓶 =倒置前 V 水 倒置后 V 空气 。
(学生在作业本上独立完成,再选代表板演在黑板上)
预设 1:3.14×(8÷2)^×7 3.14×(8÷2)^×18=1256(ml)
板书答语:瓶子的容积是 1256ml。
师:还有其他的方法吗?
师:好,老师请一名同学利用老师的学具在黑板上再演示一遍求这个瓶子容积的过程。
预设:我们可以把有水部分的圆柱体和倒置后空气部分的圆柱体拼在一起,就把瓶子的体积转化成了一个新圆柱,只要求出这个新圆柱的体积就可以了。
【设计意图:利用制作的双层学具,把有水的圆柱贴片和倒置后无水的圆柱贴片结合在一起,借助几何直观将较难理解的数学问题变得简明、形象。】
四、回顾与反思
师:回顾解决这个问题的方法和过程,你有哪些收获?
预设 1:利用体积不变的性质求瓶子的容积。
预设 2:学会了利用转化的思想求不规则物体的体积。
师:在以前的学习中我们用过转化的方法吗?
五、模仿练习
【设计意图:PPT 出示练习题目, 及时有效的练习,可以加深学生对本节课例题的理解,巩固所学知识,形成技能,启发思维,培养能力。】
五、全课小结
师:同学们:这节课你学会了什么,有哪些收获?
本文来自小学教学设计,作者为广东东莞市松山湖第一小学黄 蕊 ,文章为“第十一届小学教学特色设计大赛”获奖作品之一。选自《小学教学设计》(数学)2019年第1、2期合刊
,