因为昨天发文日期写错,小学奥数多发了一篇,今天就发一篇初中的文章,十字相乘很有用,但是教材上却没有把它放到重要位置,而且只介绍了二次项系数为1的十字相乘,所以写篇文章彻底讲下十字相乘。
1、 二次项系数为1的十字相乘
此类因式分解的模型为x2 (a b)x ab=(x a)(x b)
1.x2 6x 8 2.x2-6x 8 3.x2 2x-8 4.x2-2x-8
=(x 2)(x 4) =(x-2)(x-4) =(x-2)(x 4) =(x 2)(x-4)

基本原理:左列相乘的积为二次项,右列相乘的积为常数项,交叉相乘的积的和为一次项。
引申:如果二次项系数为负数,先把二次项系数转换为正数,然后看常数项系数和一次项系数。
· 如果常数项系数为正,一次项系数为正,则拆为两个正数相乘。
· 如果常数项系数为正,一次项系数为负,则拆为两个负数相乘。
· 如果常数项系数为负,一次项系数为正,则拆为一正一负相乘,并且正数的绝对值大。
· 如果常数项系数为负,一次项系数为负,则拆为一正一负相乘。并且负数的绝对值大。
2、 二次项系数不为1的十字相乘
此类型原理与上个类型一样,只不过把二次项系数也得拆为两个正数相乘。
此类因式分解的模型为abx2 (ad bc)x cd=(ax c)(bx d)
举例说明:2x2 13x 15=(2x 3)(x 5)
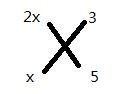
其中2x与x的积为二次项2x2 ,3与5的积为常数项,2x与5的积加上x与3的积之和为一次项。
3、 双十字相乘法
此类型原理不变,只是用2次十字相乘,应用整体思想。那么用2x2-7xy-22y2-5x 35y-3 来说明双十字方法的应用。
第一种方法:
可以把x当主元,用整理思想来分解,具体过程如下:
2x2-7xy-22y2-5x 35y-3 = 2x2 (7y 5)x -22y2 35y-3
然后先将-22y2 35y-3分解为 –(2y-3)(11y-1) =(2y-3)(-11y 1)
然后用整体思想来分解,把(2y-3) 和(-11y 1)看成2个整体。
2x2-7xy-22y2-5x 35y-3 = 2x2-(7y 5)x -22y2 35y-3
=2x2-(7y 5)x (2y-3)(-11y 1) =[x (2y-3)][2x (-11y 1)]
=(x 2y-3)(2x-11y 1)

第二种方法:
可以先分解二次项2x2-7xy-22y2 =(x 2y)(2x-11y)
然后用整体思想来分解,把(x 2y)和(2x-11y)看成2个整体。
2x2-7xy-22y2-5x 35y-3 = (x 2y)(2x-11y) -5x 35y-3
==(x 2y-3)(2x-11y 1)
,




