我们可能都知道小猴子掰玉米的故事:讲述的是一只小猴子下山时,看见一块玉米地便掰了一块玉米,没走多远又看到了桃子,便扔了玉米摘下桃子。之后又遇到了西瓜、兔子,可是最后却什么也没带回家。故事寓意是如果不能好好地把握自己手中的事物,或者贪得无厌,最终可能什么也得不到。

现在把故事简化一下:在一片玉米地里,你希望从里面选一个最大的玉米。但只能摘一次,而且不能回头,大体上你会有三种结果:
(1)你很快摘下了一个你认为比较大的玉米,然而越走越失望,因为前面还有很多比你手里的大得多的玉米。此时你已经不能够选择了,你会后悔。
(2)你发现有的玉米比之前遇到的大,你认为还有更大的,继续一直向前走,直到发现自己差不多走出了玉米地却还没有摘。但你回不去了,你仍会后悔。
(3)你摘到了最大的玉米。
生活中的情形亦是如此,每一个阶段都会面临不同的选择。到底该去哪家公司?到什么时候就要考虑结婚?什么时候就该买房子了?对于这些问题,我们会很纠结,不同的人也会有不同的选择。有人总想看看有没有更好的,有人却在一开始就确定了选项,哪一种更好?或者有没有一个最佳的选择时间点?
数学家欧拉给出一个重要的数字:37%。策略是你要把选择玉米的过程分成两个阶段。前37%的时间为第一阶段。在这个阶段,你只看不选,就是认真观察那些比较大的玉米,记住它们的大小。进入第二阶段后,你一旦遇到一个比第一阶段还要大的玉米,或者类似的玉米,就要毫不犹豫地掰下它。这个办法就叫37%法则,实际上是一个随机选择的优化问题(具体算法见文末)。
37%法则并不能保证你一定能选择到最大的玉米,但是在这片玉米地里,玉米棒子大小是随机出现的。在这种情况下,它是一个能够选到一个足够大玉米的好办法。从概率的角度来讲,如果你看了不到37%的玉米就开始选择,你将来很可能后悔选早了;如果你看了远远超过37%的玉米才开始选,你将来可能后悔选晚了。

比如买房子,你看了很多房子但只打算买一个(你选择不买,别人就会把它买走),你应该给自己设定一个看房总数的限度,或者一个时间期限。比如在一个月内一定要买到房子。根据37%法则,将一个月时间分为两个阶段。前11天为第一阶段,这个阶段只看不买,了解市场上的情况,记住你比较满意的房子。从第12天开始,一旦遇到一个比第一阶段那个比较满意的房子好或者差不多,就要毫不犹豫地买下来。

对于择偶,同样可以运用37%法则。比如,你从20岁开始找对象,设定的目标是30岁之前结婚,那么根据37%法则,两个阶段的分割点就在23.7岁。在20岁到23.7岁之间是观察期,只交往不结婚,记住你所中意的人。23.7岁之后是决策期,一旦遇到一个比以前好或者差不多好的人,就应该选择结婚。如果你的目标是40岁之前结婚,分割点就是27.4岁,即28岁以后就要有所行动。
择偶在实际生活中的选择要复杂得多,因为你有被拒的可能性,假设被拒绝的概率为50%,就要把37%变成25%。也就是说,条件不好的人要缩短观察期。反之,如果你的条件非常好,就算一开始错过了一个人,过了一段时间去找他,他还有可能答应你的话,那么你的观察期应该延长。假设这个同意的可能性是一半,那么你可以把观察期延长到61%。总的来说,条件好就可以多等等,不要急于决定;条件差的就要赶紧行动。

在生活中,很多人就败在不知道什么时候停止选择。理性的人,应该知道什么时候停止。37%法则说的是面对一个不确定的世界,在你根本不知道命运会怎样的情况下,所能采取的最佳策略。生活很复杂,算法可以帮助我们科学决策,但是选择之后更重要的是去经营好我们的选择。
今天介绍的方法来自于《指导生活的算法》,书中还总结了不少用于指导生活的实用方法,真正让算法走向了大众生活,希望对你有用。
附录:37%的由来
37% 法则源于所谓的“秘书问题”, 最优停止问题中最著名的一类难题。
“秘书问题”如下:假设一堆人申请一个秘书岗位,而你是面试官,你的目标是从这堆申请人中遴选出最佳人选。你不知道如何给每一名申请人评分,但是可以轻松地判断哪一名申请人更加优秀。你按照随机顺序,每次面试一名申请人。你随时可以决定将这份工作交给其中一人,而对方只能接受,于是面试工作就此结束。但是,一旦你否决其中一名申请人,就不能改变主意再回头选择他。对于“秘书问题”,划入观察期的人数、选中最优秀的人的概率与申请总人数之间的关系如下图所示:
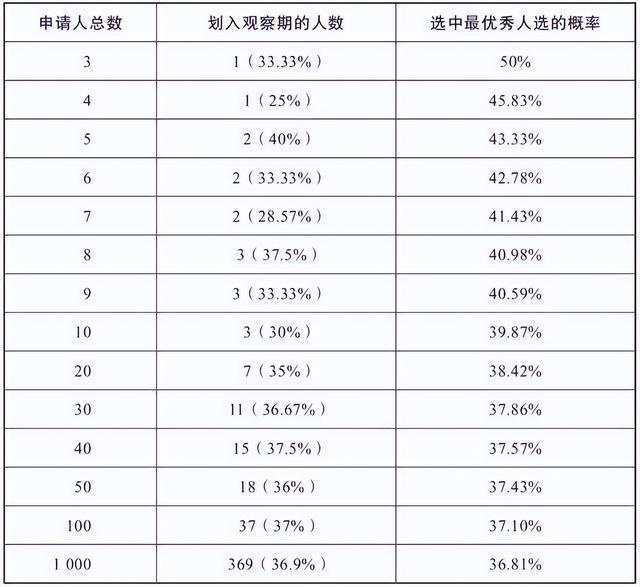
源于《指导生活的算法》
从上述表格可以看出,随着申请人数不断增加,观察与行动之间的分界线正好处在全部申请人 37% 的位置。值得注意的是,即使采用最理想的方案,也会有 63% 的概率失败,即你依然有很大的可能选错人。但是,相比于随机选取,37% 的成功率已经很高了。
更为一般的数学方法:假设这片玉米地有n个玉米,先放弃前面 k 个玉米,不管这些玉米有多大;然后从第 k 1 个玉米开始,一旦看到比之前玉米大的,就毫不犹豫地选择它。转化为数学问题就是:在玉米总数为n 的情况下,当 k 等于何值时,按上述策略选中最大玉米的概率最大?对于某个固定的 k,如果最适合的玉米出现在了第 i 个位置,k的概率记作P(k)。

用 x 来表示 k/n 的值,并且假设 n 充分大,则上述公式可以写成:

对 -x · ln x 求导,并令导数为 0,可以解出 x 的最优值,它就是欧拉数(e)的倒数—— 1/e ,大约等于 0.37(e ≈2.718281828459),因此这条法则也叫做 37% 法则。
,




