本文是吴恩达《机器学习》视频笔记第16篇,对应第1周第16个视频。
“Linear Algebra review(optional)——Matrix-matrix multiplication”
上一视频讲的是矩阵和向量相乘,我们在上上上个视频“矩阵和向量”那一节已经知道向量也是一种特殊的矩阵,那这一节我们把后面的这个向量给一般化为矩阵,即矩阵和矩阵的乘法。
引入前面讲过梯度下降用于线性回归模型的参数确定,如果有矩阵的乘法的加持,我们就可以不用梯度下降法也能求解这个问题。
先来看一个例子,求下面图中两个矩阵的乘。

那怎么做呢?上图中两个矩阵,左边的这个是2×3的矩阵、右边这个是3×2的矩阵,我们可以把右边这个矩阵的第一列抽出来,就变成了2×3的矩阵和一个3×1的列向量的乘法,这就和上一视频讲到的一样了。如下图,我们就可以得到一个2×1的列向量:
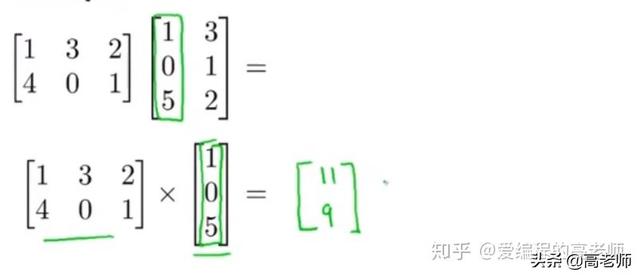
类似的,把右边矩阵的第二列抽出来相乘又得到一个2×1的列向量,然后把这两步得到的列向量拼在一起就得到两个矩阵的乘的结果了。

那上面那个特例中,左边是2×3的矩阵、右边是3×2的矩阵。右边这个矩阵的行数、列数分别和左边矩阵的列数、行数相等,是不是说一般情况也有这种要求呢?我们一起看一下。
对于一般的情况,矩阵和矩阵的乘法的形式如下图:

从上面的图中可知,矩阵A×B,只要求A的列数要等于B的行数,而不一定要求A的行数等于B的列数;得到的结果矩阵C呢,C的行数和A的行数相等、C的列数和B的列数相等。
从前面的示例我们可知,矩阵A和矩阵B的乘,可以简化为矩阵A和矩阵B的列向量的乘,然后再把结果拼成C。就完成了矩阵与矩阵的乘法。
矩阵和矩阵相乘,化简为矩阵和列向量相乘的过程中,右边的矩阵A会被用o次(即矩阵B的列数)、而矩阵B呢是被拆分成o个列向量来用的。想想这个事挺有意思的。

两个2×2的矩阵相乘,运算过程如下图:

我们来看一下,矩阵和矩阵的乘法这种运算规则的制定怎样让我们实际问题更容易被表述。
还是假设我有四套房子,面积(单位是平方英尺)不同,如下图:

这里呢,面积和售价之间关系的预测函数不再是一个了,假设我们有3个可能的公式用来计算房屋的售价,如果有矩阵乘法,就可以很方便的把这个事情给描述出来。
我们把第一个模型的参数拿出来构成矩阵B的第一列、第二个模型的参数做第二列、第三个模型的参数做第三列,就得到下图这样的一个矩阵乘法的式子。

对上面的这个式子进行运算,就可以得到一个4×3的结果矩阵。而结果矩阵的每一列就对应于相应模型对4套不同房子的售价的预测。如下图:

一次矩阵运算就可以让我们完成三个模型分别对4套房子的售价预测,即12次房屋售价预测的运算用一个矩阵乘法的式子就可以表示了,想想就让人激动。
更好的是,几乎每一种主流的编程语言都有很好的线性代数库实现矩阵与矩阵的乘法;更进一步的,如果我们想比较不同模型的好坏的话,我们只需要比较结果矩阵就行了。
我们小时候学乘法的时候知道有很多的运算法则可以使用,那么,矩阵和矩阵的乘法有没有这样的一些法则供我们使用呢?且听下回。
,




