布尔巴基建立之初的意图仅仅是写一本新的分析学教材,但他们很快就开始“雄心勃勃”起来,因为他们要为“分析学”的写作提供集合论等基础学科的“预备知识”甚至“相关知识”,但这样一来,书的覆盖面就像滚雪球一般越滚越大。谁也没有料到,迄今为止他们已经出版了三十多卷。为什么他们的事业在上世纪六七十年代前越做越大?
理由是这批现已在数学史上留下盛名的青年人一开始就有鸿鹄之志。两千年前,古希腊数学家欧几里得集前人几何成就之大成,一举写出《几何原本》(The Elements),用几乎处处无懈可击的公理体系,严密推理出几百个几何和算术定理,吹响了导致西方现代文明理性思维的号角之声,成为印刷版次数目仅次于《圣经》的不朽作品。

图1 欧几里得
到了上世纪三十年代,经过布尔巴基人一次次会议的来回争执和热烈讨论,大家一致认为,现代数学的教科书跟不上现代数学前进的步伐,尤其在饱受世界大战重创的法国,缺少统一的数学观,即他们所认定的“数学取决于结构”的哲学理念。他们要把该信条作为写作原则,把数学看成有机整体,而非各个分支的碎片组合,重新构建数学的大厦。因此,他们撇开只写出一本基于微积分思路的现代分析教科书的最初想法,决定集体写出一部与众不同、体现当代数学“结构主义”思想,充满法国文学风格的恢弘大作。
于是,他们模仿欧几里得,将书名取为《数学原本》(Elements of Mathematics) ,希望成为二十世纪的欧几里得,引领国际现代数学教育之潮流。65年后,上世纪结束,他们的目标实现得很不错。据2006年美国数学会翻译出版的 Bourbaki: A Secret Society of Mathematicians(《布尔巴基:数学家的一个秘密团体》)一书中的记载,在法文原著出版之时,已出版的书是:1.《集合论》,2. 《代数》,3. 《一般拓扑学》,4. 《单实变量函数》,5. 《拓扑向量空间》,6. 《积分学》,7. 《交换代数》,8. 《微分和解析簇》,9. 《李群和李代数》,10. 《谱理论》。其中几乎每种书都有好几卷。

图2 《数学原本》第一卷,集合论(1970版)| Wikipedia
这些书的写作过程有点像中国五十年前革命现代京剧的创作:精益求精,百炼成钢。它们都是“革新”的产物,一个属于艺术,一个属于科学,但异途同归于同样的哲学思辨。在布尔巴基集体看来,范·德·瓦尔登的《代数学》是数学写作的典范,于是决定每个章节写出像它那样的风格。但是范·德·瓦尔登写书的依据是诺特 (Emmy Noether,1882-1935) 和阿廷 (Emil Artin,1898-1962) 的讲义,他不必受到别人七嘴八舌的干扰,而以一己之力独自完成那本杰作。(参看《一百年前,她成为德国历史上第一位女性数学讲师》)
布尔巴基就不同了,他们是“写作班子”。每本书动笔之前,大家在会上讨论怎么写,写哪些,以及材料布局的先后次序,等等,都要由众人各抒己见,出谋划策,任何成员都像联合国常任理事国那样拥有否决权,只有一致同意后才决定开写。这时一位志愿者接下任务,由他无拘无束地按照大家定下的模糊计划写出初稿。一两年后,初稿在布尔巴基会议上宣读。在“审稿”会上,他们如同遵循美国杰出数学家费德勒 (Herbert Federer,1920-2010) 关于修改自己数学作品的忠告“好像你是作者最凶恶的敌人”似的,对初稿百般挑剔,无情批判,结果是一部稿子体无完肤地落荒而去,于是再写第二稿,甚至第三稿第四稿,乃至第六、第七、第八稿。读者最后看到的出版物,就是这样千锤百炼后出炉的产品。
前已所述,布尔巴基人信奉“结构主义”思想。他们认为数学研究的是结构:代数结构、拓扑结构和序结构。代数结构关心的是代数运算,拓扑结构与“连续”的概念有关,是分析学研究的对象,而序结构像实数那样考虑的是大小关系。布尔巴基所写的几十卷书全是遵循结构主义思想的结晶,这些精心打造的著作,注重理论概念的结构分析,对不同结构分门别类,全书材料经过整理归纳,各就各位,论题所在位置恰到好处,具有严密的逻辑性,对同时代及后世的数学家及学生影响极大。从欧洲到亚洲,从北美洲到南美洲,许多数学家长大成人的养分就是一部接着一部的布尔巴基大书!
布尔巴基的活动作为一个数学团体,虽然是“半秘密”性的,布尔巴基有自己公开的数学活动。自从1935年7月历时一周的第一次全体会议开始,直到1939年,这样的会每年一次。第二次世界大战爆发后,会员无法聚会,但零星联系依然存在,大战结束后又恢复了所有活动。直到1948年美国洛克菲勒基金会开始提供资助前,布尔巴基的成员都是自掏腰包参加活动,充分说明他们对数学的无比热爱。
不像正式的数学团体,布尔巴基也没有什么“学会章程”之类的繁文褥节。它的正式成员制度,体现了“数学是年轻人的事业”这一信条,“到了50岁必须退出”是一项不成文的规定。年轻的数学人想参加活动,悉听尊便,但要想成为新成员,必须有经得起布尔巴基讨论数学时燃起的熊熊烈火炙烤的心理准备,而且要有添加燃料让火烧得更旺的激情才行。那些坐在一旁洗耳恭听沉默不语的胆小人物或对数学不太活跃的落后分子,多半不会再被邀请参加活动。多年来,布尔巴基的正式成员一般维持在一打左右。
法国和苏联数学界都有讨论班的传统,法国有阿达马的讨论班和朱利亚 (Gaston M. Julia,1893-1978) 的讨论班,苏联有柯尔莫哥洛夫 (Andrey Kolmogorov,1903-1987)的讨论班和盖尔范德 (Israil Gelfand,1913-2009) 的讨论班。从1948年起,布尔巴基开始举办讨论班,每年2、6、11月共三次在周末举行,每次五个邀请报告,约有200人参加。报告的内容都是数学各方面的最新结果,最后结集出版。今年最后的一次布尔巴基讨论班,报告的内容有北京国际数学研究中心博士后韦东奕与合作者的成果。
布尔巴基的影响通过几十卷数学著作的出版,布尔巴基成了上世纪影响力最大的数学学派之一,其声誉在六七十年代达到顶峰。
韦伊一开始就锁定了巴黎的出版社Hermann同他们携手同进。编辑Enrique Freymann早先就出版过谢瓦莱和韦伊为纪念英年早逝的一位杰出逻辑学家而编辑的一本论文集,后来为布尔巴基丛书的大卖立下汗马之功。事实上,谢瓦莱甚至宣称这位出版人很早就鼓励他们两人写出分析教程以取代古尔萨。尽管有冒险的可能,Freymann一开始就以极大的热情支持布尔巴基的事业。对他至死不渝地全力相助,布尔巴基深受感动,将1954年出版的《集合论》第一卷献给了校对清样时不幸去世的他。
布尔巴基的数学观与现代数学三大学派之一的形式主义学派相一致,他们是德国人希尔伯特的门徒,而不是法国人庞加莱的接棒者。公理体系与抽象的结构主义是他们几十年如一日挥舞的两面旗帜。他们信奉的是:数学的统一性,公理方法,以及结构的研究。这在他们于1947年以尼古拉·布尔巴基署名的文章《数学的结构》中有进一步的阐述。他们所撰的数学书,将现代纯粹数学大厦的中央大厅、砖瓦结构、门窗走廊、天花板面、悬梁屋檐等建筑要素一一展示,有机结合,极富数学建筑之美。精工细作的写作态度使得几乎每本都是登峰造极之作,再加上出版商的通力合作,在数学家与出版社直到七十年代为止的蜜月期间,《数学原本》各卷出版后的销售蒸蒸日上,不仅众多的数学工作者购买,而且全世界的图书馆也要馆藏一本,在很长一段时间内成了出版社的主要利润来源。

图3 左为希尔伯特,右为庞加莱 | Wikipedia
然而,如果以为布尔巴基的主要成就仅仅只是十来种30多卷的大书,那就大错特错了。布尔巴基的成员,无论是奠基者还是中生代,甚至年轻一代,许多都是顶级的数学家,其中名气最大的大概就是韦伊了,他是上个世纪全世界几个最伟大的数学家之一,在代数数论和代数几何领域的深刻工作影响深远。同是奠基者的迪厄多内,是这个数学圈子的主要写手,一生在多个领域勤奋耕作,著作等身,晚年还写出泛函分析等学科的数学史。他自己的一本书《现代分析基础》(Foundations of Modern Analysis),七十年代末被南京大学数学系选为研究生的教材,而那时我班两位醉心纯粹数学的同学——田刚和王宏玉——则旁听了这门课,按照授课老师之一的苏维宜教授所述,他们两人的考试成绩全班最高。可见布尔巴基及其成员对远在东方的年轻学子也产生了持续终生的影响。
几乎所有的法国菲尔兹奖获得者都是布尔巴基后来的成员,如施瓦尔兹 (Laurent Schwartz,1915-2002) 、塞尔 (Jean-Pierre Serre,1926-) 、格罗腾迪克以及英年早逝的动力系统大家约科兹 (Jean-Cristophe Yaccoz,1957-2016) 。在分形领域做出杰出贡献的德奥迪 (Adrien Douady,1925-2006) 也在其中。早期的成员中,唯一的外国人艾伦伯格 (Samuel Eilenberg,1913-1998) 来自波兰,后来长期在美国。他和美国数学家麦克莱恩 (Saunders MacLane,1909-2005) 创造的范畴论,现在是理论物理学界炙手可热的数学工具。
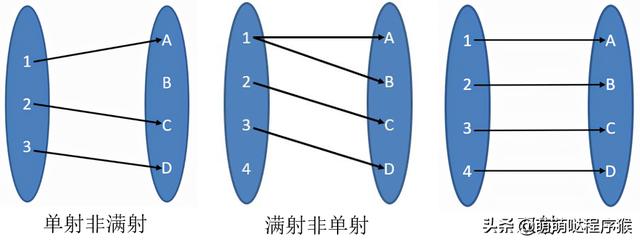
布尔巴基不仅以它的数学与写作影响了全世界,风行了几十年,而且创造了一些数学概念和符号,其中许多“一夜成名”,比如原创法文的filtre和英文翻译filter。最有名的例子就是空集的符号Ø,它由韦伊所独创。现已广泛使用的三个函数术语“单射” (injection) 、“满射” (surjection) 及“双射” (bijection) ,也是布尔巴基的发明。
作为数学家群体的布尔巴基,其影响力也进入了艺术界,对结构主义的艺术流派有一定的影响。但是,它对初等数学教育的影响却导致了七十年代轰轰烈烈的“新数学”运动的诞生。“新数学”要打倒欧几里得,要把“集合论”请进中小学的课堂。然而,这个影响却是负面的,因为“新数学”的实践结果几乎是一场灾难。旅居美国在约翰斯·霍普金斯大学教书的日本数学家小平邦彦 (1915-1997) 目睹自己的女儿成了这场试验的牺牲品,在他的《惰者集》一书中对“新数学”大加鞭挞!

图4 《惰者集》
从历史的角度看,布尔巴基对整个数学贡献巨大,影响了几代数学家。但是,它的数学观和哲学思想也一直饱受批评。其中最激烈的讨伐者大概非俄罗斯数学家阿诺德 (Vladimir Arnold,1937-2010) 莫属。就数学哲学而言,阿诺德是庞加莱的信徒,而不是希尔伯特的粉丝,当然这不妨碍他解决了后者的“23个问题”中的一个。这位柯尔莫哥洛夫的杰出弟子个性独特,言语锋利,批评起来不留情面。我在他的一篇文章中读到,他面试一位求职的法国数学家,后者的专业是线性代数,却答不出“二次型xy的符号差为几”这个简单问题。这名法国教授也许读了太多的布尔巴基著作,过分重视“一般性”而忽略了“具体性”,而这正是阿诺德所最反对的。阿诺德大概最欣赏一句名言——“艺术源于生活,但高于生活”。他认为数学是现实世界的反映,而不是先有数学结构再将之套用到现实世界中去。他自己的一句名言是:“数学是物理的一部分。”
这也从另一个方面验证了布尔巴基的缺陷:太注重纯粹数学而忽视应用数学,比如现在特别热门的统计学就不在他们撰著的考虑范围之内。这也是许多数学家批评的另一方面。具有讽刺意义的是,布尔巴基最年长的创始人芒德布罗伊的侄子芒德布罗,却是反对布尔巴基的急先锋。30岁不到时,他甚至逃离祖国而去了美国,六十年代在那里开创了布尔巴基大概不甚欣赏的分形几何学。
今天,距离布尔巴基第一次工作会议的日子已经过去85年了。它的成长史和兴衰史,它对世界数学的不朽功勋和消极影响,都对中国数学界有启示作用。现代数学的发展和应用,应该是牛顿-庞加莱与哈代-希尔伯特的对立统一,应该是具体与抽象的相辅相成,应该是应用与理论的有机结合。这大概是中国数学努力赶超世界先进水平的一条可行之路吧。
注:本文转自公众号“中国数学会”
,