根据机器学习的任务或应用情况的不同,我们通常把机器学习分为三大类:
1、监督学习(Supervised Learning,SL),这类算法的工作原理是使用带标签的训练数据来学习输入变量

转化为输出变量
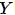
的映射函数,换句话说就是求解方程

。进一步地,监督学习又可细分为如下三类:
- 回归(Regression):预测一个值,如预测降雨量、房价等,较基础的算法有:Linear Regression
- 分类(Classification):预测一个标签,如预测“生病”或“健康”,图片上是哪种动物等,较基础的算法有:Logistic Regression、Naive Bayes、K-Nearest Neighbors(KNN)
【另】:集成(Ensembling)也可以归类为监督学习的一种,它将多个单独较弱的机器学习模型的预测结合起来,以产生更准确的预测,较基础的算法有Bagging with Random Forests、Boosting with XGBoost
2、非监督学习(Unsupervised Learning,UL),这类算法的工作原理是从无标签的训练数据中学习数据的底层结构。进一步地,非监督学习又可细分为如下三类:
- 关联(Association):发现集合中项目同时出现的概率,如通过分析超市购物篮,发现啤酒总是和尿片一起购买(啤酒与尿片的故事),较基础的算法有:Apriori
- 聚类(Clustering):对数据进行分组,以便组内对象比组间对象更相似,较基础的算法有:K-means
- 降维(Dimensionality Reduction):减少数据集的变量数量,同时保证重要的信息不被丢失。降维可以通过特征提取方法和特征选择方法来实现,特征提取是执行从高维空间到低维空间的转换,特征选择是选择原始变量的子集,较基础的算法有:PCA
3、强化学习(Reinforcement Learning,DL),让agent根据当前环境状态,通过学习能够获得最大回报的行为来决定下一步的最佳行为。
实现以上列出的算法都是简单常用的,基于scikit-learn可以仅用几行代码就完成模型训练、预测、评估和可视化。关于算法的原理知乎上有很多精彩的回答,这里不会赘述,仅给出代码的实现与可视化。
Linear Regression
它为变量分配最佳权重,以创建一条直线或一个平面或更高维的超平面,使得预测值和真实值之间的误差最小化。具体原理参考:用人话讲明白线性回归LinearRegression - 化简可得的文章 - 知乎。下面以一元线性回归为例,给出代码实现。

Logistic Regression
虽然写着回归,但实际上是一种二分类算法。它将数据拟合到logit函数中,所以称为logit回归。简单来说就是基于一组给定的变量,用logistic function来预测这个事件的概率,给出一个介于0和1之间的输出。具体原理参考:用人话讲明白逻辑回归Logistic regression - 化简可得的文章 - 知乎,下面给出代码的实现。

Naive Bayes
朴素贝叶斯是一种基于贝叶斯定理的分类方法,它会假设一个类中的某个特征与其他特征无关。这个模型不仅非常简单,而且比许多高度复杂的分类方法表现得更好。具体原理参考:朴素贝叶斯算法原理小结 - 刘建平Pinard,下面给出代码的实现。


K-Nearest Neighbors
这是用于分类和回归的机器学习算法(主要用于分类)。它考虑了不同的质心,并使用欧几里得函数来比较距离。接着分析结果并将每个点分类到组中,以优化它,使其与所有最接近的点一起放置。它使用k个最近邻的多数票对数据进行分类预测。具体原来参考:K近邻法(KNN)原理小结 - 刘建平Pinard,下面给出代码的实现。

Decision Tree
遍历树,并将重要特征与确定的条件语句进行比较。它是降到左边的子分支还是降到右边的子分支取决于结果。通常,更重要的特性更接近根,它可以处理离散变量和连续变量。具体原理参考:深入浅出理解决策树算法(一)-核心思想 - 忆臻的文章 - 知乎,下面给出代码的实现。

Random Forest
随机森林是决策树的集合。随机采样数据点构造树、随机采样特征子集分割,每棵树提供一个分类。得票最多的分类在森林中获胜,为数据点的最终分类。具体原来参考:独家 | 一文读懂随机森林的解释和实现 - 清华大学数据科学研究院的文章 - 知乎,下面给出代码的实现。


Support Vector Machines
它将数据映射为空间中的点,使得不同类别的点可以被尽可能宽的间隔分隔开,对于待预测类别的数据,先将其映射至同一空间,并根据它落在间隔的哪一侧来得到对应的类别。具体原来参考:看了这篇文章你还不懂SVM你就来打我 - SMON的文章 - 知乎,下面给出代码实现。

import matplotlib.pyplot as pltimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.datasets import make_classification
# SVMfrom sklearn import svm# 1. 准备数据svm_X_train, svm_y_train = make_classification(n_features=2, n_redundant=0, n_informative=2, random_state=1, n_clusters_per_class=1, n_classes=4)# 2. 构造训练与测试集l, r = svm_X_train[:, 0].min() - 1, svm_X_train[:, 0].max() 1b, t = svm_X_train[:, 1].min() - 1,svm_X_train[:, 1].max() 1n = 1000grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n))svm_X_test = np.column_stack((grid_x.ravel(), grid_y.ravel()))# 3. 训练模型# svm_model = RandomForestClassifier(max_depth=4)svm_model = svm.SVC(kernel='rbf', gamma=1, C=0.0001).fit(svm_X_train, svm_y_train)svm_model.fit(svm_X_train, svm_y_train)# 4. 预测数据svm_y_pred = svm_model.predict(svm_X_test)# 5. 可视化grid_z = svm_y_pred.reshape(grid_x.shape)plt.figure('SVM')plt.title('SVM')plt.pcolormesh(grid_x, grid_y, grid_z, cmap='Blues')plt.scatter(svm_X_train[:, 0], svm_X_train[:, 1], s=30, c=svm_y_train, cmap='pink')plt.show()
K-Means
将数据划分到K个聚类簇中,使得每个数据点都属于离它最近的均值(即聚类中心,centroid)对应的集聚类簇。最终,具有较高相似度的数据对象划分至同一类簇,将具有较高相异度的数据对象划分至不同类簇。具体原理参考:用人话讲明白快速聚类kmeans - 化简可得的文章 - 知乎,下面给出代码的实现。

import matplotlib.pyplot as pltimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.datasets.samples_generator import make_blobs
# K-means 任务为聚类 n_classes=5from sklearn.cluster import kmeans
# 1. 准备数据kmeans_X_data, kmeans_y_data = make_blobs(n_samples=500, centers=5, cluster_std=0.60, random_state=0)# 2. 训练模型kmeans_model = KMeans(n_clusters=5)kmeans_model.fit(kmeans_X_data)# 3. 预测模型kmeans_y_pred = kmeans_model.predict(kmeans_X_data)# 4. 可视化plt.figure('K-Means')plt.title('K-Means')plt.scatter(kmeans_X_data[:,0], kmeans_X_data[:, 1], s=50)plt.scatter(kmeans_X_data[:, 0], kmeans_X_data[:, 1], c=kmeans_y_pred, s=50, cmap='viridis')centers = kmeans_model.cluster_centers_plt.scatter(centers[:,0], centers[:, 1], c='red', s=80, marker='x')plt.show()
PCA
一种常用的降维技术,顾名思义,PCA帮助我们找出数据的主要成分,主成分基本上是线性不相关的向量,用选出的k个主成分来表示数据,来达到降维的目的。具体原理参考:如何通俗易懂地讲解什么是 PCA 主成分分析?- 马同学的回答 - 知乎,下面给出代码实现。
import matplotlib.pyplot as pltimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.datasets import make_classification
# PCAfrom sklearn.decomposition import PCAfrom sklearn.datasets import load_iris
# 1. 准备数据pca_data=load_iris()pca_X_data=pca_data.datapca_y_data=pca_data.target# 2. 训练模型, 维度为2pca_model=PCA(n_components=2) # 3. 降维reduced_X=pca_model.fit_transform(pca_X_data)# 4. 可视化red_x,red_y=[],[]blue_x,blue_y=[],[]green_x,green_y=[],[]
for i in range(len(reduced_X)): if pca_y_data[i] ==0: red_x.append(reduced_X[i][0]) red_y.append(reduced_X[i][1]) elif pca_y_data[i]==1: blue_x.append(reduced_X[i][0]) blue_y.append(reduced_X[i][1]) else: green_x.append(reduced_X[i][0]) green_y.append(reduced_X[i][1])
plt.figure('PCA')plt.title('PCA')plt.scatter(red_x,red_y,c='r')plt.scatter(blue_x,blue_y,c='b')plt.scatter(green_x,green_y,c='g')plt.show()
至此,给出了常有的9种机器学习算法的实现,题主可以通过一些实际案例去进一步理解和熟悉算法。国外的Kaggle和阿里云天池都是获取项目经验的好途径。
原文链接:http://click.aliyun.com/m/1000298227/
本文为阿里云原创内容,未经允许不得转载。
,




