我们听过的很多动人心魄的神话可能是始于一个真实的故事,它曾在历史的某个时间点上真实地发生过,但在代代相传的传颂中,被一点一点的蒙上传奇的色彩,让真相被一点一点地被抛在脑后。神话之所以总能在人们心中存留和演化,或许是因为它们多少承载着一些隐藏的真理,能够满足人类在心灵上的某些需求。
以严谨的逻辑著称的数学似乎是神话的一个对立面,但有时,一些数学真理会在缺乏理解的复述之下,以“神话”般的形式进入到公众意识。今天我们要说就是数学中的一则“神话”——黄金比例(黄金分割率)。
什么是黄金比例?
黄金比例是一个神奇的常数,我们通常用希腊字母φ来表示它。它出现在很多文学和艺术作品中,比如在小说和电影《达芬奇密码》就提到了这个有着神秘色彩的数字。之所以说它神秘,是因为与数学中的许多其他概念相比,这个数字的确有着更多的“神话”:它被许多作家描述为是自然界所有美丽图案的基础,是神圣的比例;也被称为是许多艺术作品和建筑物的设计基础,如希腊的帕特农神庙和埃及的金字塔。
黄金比例最早出现在欧几里得的著作《几何原本》中,欧几里得将它定义为:

那么,φ究竟等于多少呢?我们知道,a / b = φ,且 (a b) / a = φ,因此上图中的等式可以变成:

对这个方程进行求解,就能得到:

由于φ必须大于1, 所以我们取φ = 1.61803…它是一个无理数,这并不难理解,因为根号5正是一个无理数,也就是说它是一个无法被写成两个整数之比的数。这是黄金比例的一个非常重要的性质。
一维的黄金比例还可以延伸为所谓的黄金矩形,我们可以根据以下步骤画出一个黄金矩形:
1、首先需要画一个边长为a的正方形;2、然后取正方形的一条边(比如底边)的中点:以该中点为圆心,以中点到与对边相连的一个顶点的距离为半径画圆;3、延长底边,让它与圆弧相交,得到的交点便是黄金矩形的一个角。

除了黄金矩形之外,黄金比例φ还有另一个可爱的几何表达,那就是它是一个边长为1的正五边形的对角线的长度。(读者可以试着用余弦定理来检验哟!)
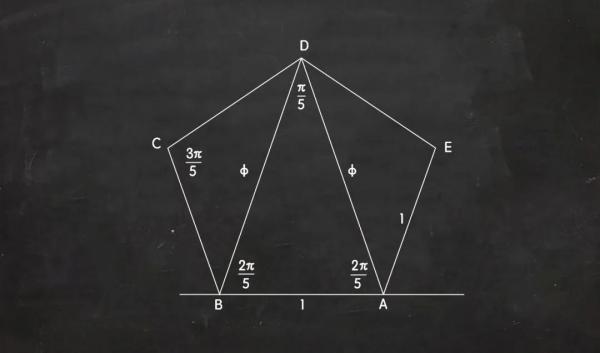
如上图所示,由对角线和底边形成的边长为1、φ、φ的等腰三角形BAD,被称为黄金三角形,它在五重对称的研究中频繁出现,例如五角星就是由五个黄金三角形构成的:

其实,定义黄金比例的方法有很多,一个非常著名的例子是斐波那契数列:

这个序列中的下一项是前两项之和,是由斐波那契提出的一种用来理解兔子种群增长的方法,它在理解人口增长方面具有重要作用。
这个数列是如何与黄金比例联系在一起的呢?最早发现这一惊人秘密的是开普勒(Johannes Kepler),他注意到,如果取这个序列中的两两相连的数字之比(后一项比前一项),得到的比值就可以形成数列:

而这个数列最终会收敛到一个熟悉的数字——1.618… 这个数列的极限正是黄金比例。
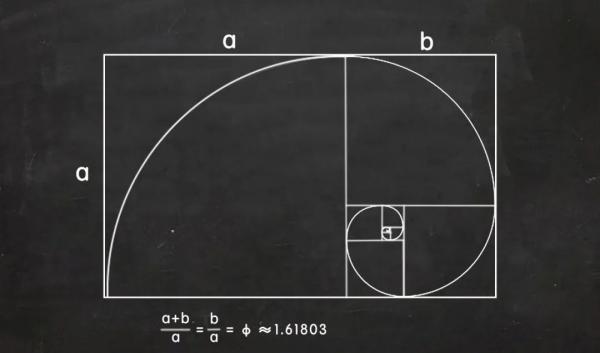
黄金比例的无理性,使我们可以在黄金矩形中看见能无限循环下去的斐波那契数列的比。
被“神”化的黄金比例
黄金比例是一个有趣的数字,它有很多奇特的性质,也有许多有用的应用。这些奇特的性质吸引了一些数学家的关注,然而对于公众而言,它的这些属性却意外的被提升到了一个不恰当的位置。
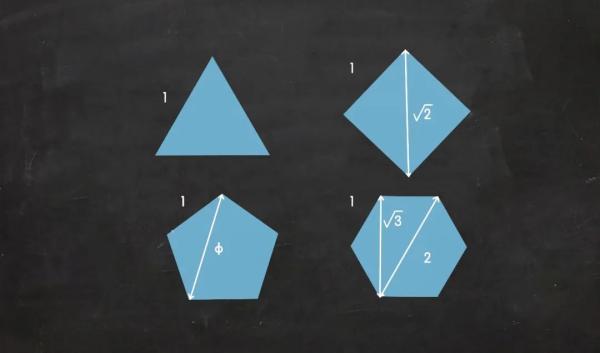
在数学家眼中,重要的常数有很多,比如√2——它是边长为1的正方形的对角线长度,也是一张A4纸的长宽比例。其实1、√2、√3在几何中的出现频率都远高于φ。
说起重要的常数,还有两个不得不提的数字便是π和e,无论是在数学世界还是现实世界,它们都有着不言而喻的重要性。

在几何学中,圆周率π是圆周长与直径之比,它的应用远远超出了几何学,它出现在数学的所有领域,从微积分到数论,从统计学到量子力学。数字e是另一个在数学中扮演着同等重要角色的常数,它是微积分的基本要素,它与任何关于增长的事物有关。在科学和工程学的许多重要公式中,都有π和e的身影,这两个数字和宇宙密切相关。
相比之下,φ的应用场景要少得多。然而在普及数学时,φ的神秘色彩使其所享有的“荣耀”远多于这两个宇宙的核心数字。需要强调的是,这并不是说φ不重要(我们将在第3部分讨论黄金比例的真正神奇之处),只是说它在数学和科学中所扮演的角色与传说中的大相径庭。
为什么φ在大众媒体上会获得如此显赫的地位呢?可能就像所有神话的流传一样,一次次的神化原因早已遗失在历史的长河中了。但仍可以照着一些线索探寻其中的一些故事。
隐藏在自然中的黄金比例?
黄金比例以多种形式出现在自然界中。前面我们已经提到,黄金比例与斐波那契数列密切相关。而斐波那契序列在自然界中是真实存在的,因为它既与种群的增长方式有关,也与形状可以组合在一起的方式有关。
例如,在太阳花的螺旋中我们可以看到这个序列(下图左),它们以一种可以捕捉到最多阳光的有序方式排列在一起;再比如,从蜂箱中的雄蜂与雌蜂的数量分布中(下图右),我们也可以观察到这种由蜜蜂的繁殖方式所产生的接近φ的比率。

然而,还有很多情况下,黄金比例被不恰当地联系到了一起。比如很多人说完美的人体比例、完美的脸型等都与φ有关。事实上,人体有许多可能的比率,其中大多介于1和2之间,而且这些“完美”的度量是没有清晰定义的,如果你细想,完美的人体比例还可能接近1.6、5/3、3/2,√2、21/13等等。而这些其实都只是人类大脑感受的一些假相关而已。当我们用从数据中发现的假相关性来论证一个观点时,这实际上可能是非常危险的,比如在法律审判中,假相关有可能会导致错误的指控,甚至错误的定罪。
黄金螺旋是螺旋吗?

上图中所示的黄金螺旋或许是与黄金比例联系得最为紧密的一个例子,它近似于一个螺旋。你只需无限地取越来越小的黄金矩形中的圆弧,就能得到这样一个图案。
在很多地方,这种形状被套用在自然和艺术之上,比如鹦鹉螺的形状、星系的形状、飓风的形状、甚至海浪的形状:

然而问题在于,黄金螺旋并不是螺旋!它是由一系列的圆弧构成的图案,从一个弧过度到一个弧,螺旋的曲率会出现跳跃,这是在任何自然现象中都不太可能出现的跳跃。在最好的情况下,黄金螺旋可以近似为一个真正的螺旋,它所近似的是对数螺旋的一个例子,这种对数螺旋在自然界中很常见,并且可以用极坐标方程表示为:

在自然界中,这样的螺旋随处可见,b值对应于不同的实际情况,这对b的任何值都成立,与黄金比例无关。黄金螺旋对应的b值为:

这个数字没有任何特别。鹦鹉螺的壳是一种对数螺线,因为这种自相似性能使它在不改变形状的情况下生长,它的最常见b值是0.18,与黄金螺旋的b值相去甚远。
艺术与建筑中的比例
人们认为,黄金比例在美学上更令人赏心悦目,因此在很多艺术和建筑作品中,黄金矩形也比其他矩形更受青睐。不可否认,一些艺术家和建筑师的确会将黄金比例融入到作品中,但这也是黄金比例概念被过度套用的领域。
理性说来,黄金矩形令人愉悦本就是一个证据薄弱的陈述。有心理学研究表明,人们对于长方形的偏好范围很广,各种比例都有其受众人群,而其中最受欢迎的是长宽比为√2比1的矩形。斯坦福大学数学家和科普作家Keith Devlin曾在美国数学协会的一个专栏中写道,黄金比例与美学之间的关系之所以如此深入人心主要因为两个人,一个是意大利数学家卢卡·帕西奥利(Luca Pacioli),另一个是德国心理学家阿道夫·泽辛(Adolf Zeising)。
卢卡·帕西奥利是达芬奇的朋友,他在1509年写了一本名为《神奇的比例》的书,这本书虽然以黄金比例为题,但并没有基于黄金比例主张任何美学理论。另外,经常有人说达芬奇在画作中用到了黄金比例,最著名的例子是画作《维特鲁威人》,然而这些比例与黄金比例并不相符,没有直接证据证明达芬奇用到了这种比例,他只是在他的作品中提到了整数比。
泽辛曾将黄金比例描述为“自然和艺术领域的美丽和完整……它是一种至高无上的精神理想,渗透到所有的结构、形式和比例中,无论是宇宙的还是个人的、有机的还是无机的、声学的还是光学的。”然而,这种说法继而影响了许多其他人,为“黄金比例”这一现代神话奠定了基础。
还有观点称,黄金比例在音乐作曲中也很重要。然而与艺术和建筑一样,几乎没有任何证据可以证明这一观点。与音乐紧密相连的数字是2的12次方根,不是黄金比例。
这种夸大的“神话”其实很令人不安,它会误导很多人,让人们对数学的运作产生错误的认识。当那些深信这些神话的人发现事实并非如此时,可能会对数学解释世界的真实能力失去信心。
黄金比例的真正神奇之处
如果前面说的都是在给黄金比例摘到“神奇”的帽子,接下来我们要说的就是黄金比例的真正神奇之处。
毫无疑问,黄金比例在数学和科学中是一个非常奇妙的数字,而真正让它有别于其他数字的一个重要属性是它的无理性。前面我们说道,φ是一个无理数,也就是说它无法被表示成任何分数,然而更令人惊讶的是,那就是它是无理性最强的一个无理数。这意味着它不仅不能被精确地表示为分数,甚至很难用分数来近似。这是一个非常特殊的性质。
为什么说φ是无理性最强的一个数字呢?数学家在对一个无理数进行近似时,会用到由两个整数(m和n)组成的分数m/n,对任意无理数z来说,不同的n值对应不同的m值。要找到z的最佳近似,则是要找出能使z与近似分数之差的绝对值,|z - m/n|,最趋近于0的n,换句话说,就是找到近似误差最小的n。

上图中所比较的是π(红)和φ(蓝)的近似误差图,横坐标轴表示的是n从1到200的取值,纵坐标是无理数与近似值之差 “Error =|z - m/n|”。可以看出,对于π来说,当n=7和n=113时,能给出非常好的π的近似。这也正是我们所熟知的 π ≈ 22/7和355/113。
与π相比,黄金比例φ的近似情况显然没有那么明朗。它的近似误差曲线比其他无理数的近似误差曲线收敛得更慢。而这背后的原因,是因为φ具有一个特殊性质——它可以被表示为一个“连分数”,使得φ可以被写成这样一种形式:

它是恒等式 φ - 1 = 1/φ 的一个直接推论。
φ的连分数形式有一个关键的特征,那就是每一项都有1存在,这些分母中所包含的1会导致较大的误差,从而使得整个分数收敛缓慢。
相比之下,π的连分数是这样的:

可以看到它的分母中的数字都很大,比如7、15 、292等等。这些大的数字会使连分数的误差小得多。
然而,这种用分数对φ进行近似的困难程度,也使它成为了数学家和计算机科学家在研究同步过程时的一个非常有用的数字。可以说,虽然黄金比例不同于公众所想象的那般神奇,但当你了解了它真实的样子之后,或许会更加惊叹于数学的真正魅力!
本文节选并整理自数学家Chris Budd于2020年02月11日,在格雷沙姆学院(Gresham College)发表的演讲《伟大的数学神话》(Great Mathematical Myths),在Budd的演讲中,他还提到了著名的三门问题和四色定理等,全文链接可参阅:gresham.ac.uk/lectures-and-events/great-maths-myths
封面图来源:mayeesherr. / Flickr
声明:转载此文是出于传递更多信息之目的。若有来源标注错误或侵犯了您的合法权益,请作者持权属证明与本网联系,我们将及时更正、删除,谢谢。
,




