例1、图中ABCD是个直角梯形,以AD为一边向外作长方形ADEF,其面积为6.36平方厘米。连接BE交AD于P,再连接PC。则图中阴影部分的面积是多少平方厘米?

阴影面积由① ②组成
∵②、③是等底等高的三角形
∴ ②=③
∴只要求① ③就行了
∵ ① ③与AED是等底等高的三角形
∴阴影面积=AED的面积=长方形面积的一半=6.36÷2=3.18
例2、如图,正方形ABCD和正方形ECGF并排放置,BF与CD相交于H,已知AB=6,则阴影部分的面积是多少?
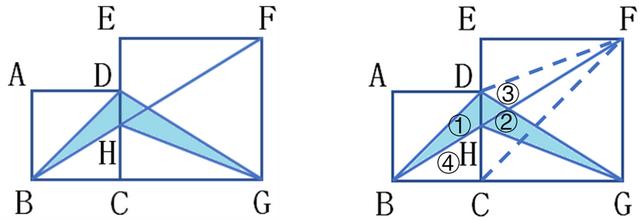
阴影面积由① ②组成
∵②、③是等底等高的三角形
∴ ②=③
所以只要求① ③就行了(还是无法求,还得等积变形)
在梯形BDFC中,
∵① ③与① ④是等底等高的
∴S阴= ① ④=ABCD的一半=6×6÷2=18
例3、如图,长方形 ABCD =120,S阴=80 。求四边形EFGH的面积。

∵②③④与ABE是等底等高的,
①③⑤与DEC也是等底等高的
∴②③④ ①③⑤=ABE DEC=半个长方形面积=60
∵ ②③④ ①③⑤ S阴=长方形面积 ③( ③重复算了一遍)
∴60 80=120 ③
∴③=20
例4、S△MBE=13cm²,S△FGD=35cm²,SAENF =49㎝²,ABCD为平行四边形,求S阴。

分析:解题关键在于对平行四边形的一半模型熟悉。
∵S阴 ① ②=半个平行四边形
(13 49 ①) (35 ②)=半个平行四边形
∴ S阴 ① ②= (13 49 ①) (35 ②)
∴S阴=13 49 35=97
,




