有关线段最值是近年来中考数学热点题型,也是教学中的难点,对于有关线段和之最值,我们常常会想到将军饮马,那么有关于单条线段的最值可能较多的还是圆。我们先来看看圆有关基本知识吧,圆的定义:在同一个平面内,到定点等于定长的点的集合就是圆。那么既然圆最大的特点就是半径相等,那么点与圆上各点间距离比较就显而易见了。

情形1:P为圆O外一定点,则点P与圆心O距离为定值,那么P点与圆上各点的连接线段中,最小值为图1中PA,最大值为图2中PA.


情形1的动态演示
情形2:P为圆O内一定点,则点P与圆上各点的连接线段中,最小值为图4中PA,最大值为图5中PA.


情形2的动态演示
情形3:P为圆上一定点,其到圆上其它各点的连接线段中,最大值为直径,最小值为0.
模型特征总结:一箭穿心(所在的直线必经圆心)

例题1.如图,Rt△ABC中,AB⊥BC,AB=8,BC=3,P是△ABC内部的一个动点,且满足∠APB=90°,则线段CP长的最小值为 .

【分析】首先证明点P在以AB为直径的⊙O上,连接OC与⊙O交于点P,此时PC最小,利用勾股定理求出OC即可解决问题.解题的关键是确定点P位置,学会求圆外一点到圆的最小、最大距离,属于中考常考题型.
【解答】∵AB⊥BC,∴∠ABC=90°,
∵∠APB=90°,∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此

变式1.如图,Rt△ABC中,AC⊥BC,AC=8,BC=12,P是△ABC内部的一个动点,且满足∠PCA=∠PBC,则线段AP长的最小值为 .

【解析】利用∠PCA=∠PBC得∠PBC ∠PCB=90°,则∠BPC=90°,根据圆周角定理的推论可判定点P在以BC为直角的⊙O上,连接OA交⊙O于P,此时PA的长最小,然后利用勾股定理计算出OA=10, 所以PA长的最小值为10﹣6=4.故答案为4.

例题2.如图,菱形ABCD边长为4,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A1MN,连接A1C,则A1C的最小值是 .
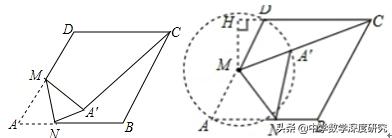
【分析】根据题意得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可,解题的关键是学会添加常用辅助圆,构造直角三角形解决问题,不同的突破点是正确寻找点A′的位置.
【解答】由折叠知A′M=AM,又M是AD的中点,可得MA=MA′=MD,做点A′在以AD为直径的圆上,如图2,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H
∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
∵在边长为4的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=4,∠HDM=60°,∴∠HMD=30°,

变式2-1.如图,在边长为8的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一点,将△AMN沿MN所在的直线翻折得到△A'MN,连接A'B,则A'B的取值范围 .
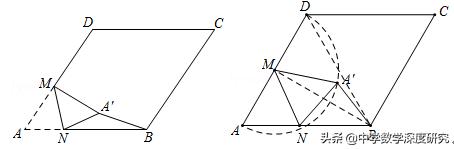
【解析】连接BM,BD,依据M是边AD的中点,△AMN沿MN所在的直线翻折得到△A'MN,即可得到点A'的轨迹为以AD为直径的半圆M,依据A'B A'M≥BM,即可得出A'B≥BM﹣A'M=4√3﹣4,当点N与点A或点D重合时,A'B的最大值为8,即可得到A'B的取值范围4√3﹣4≤A'B≤8.
变式2-2.如图,在菱形ABCD中,∠D=60°,AB=2√3,P为△ACD内一点,连接AP,BP,BP与AC交于点G,且∠PAG=∠PBC.E为AD边上一动点,则CE PE的最小值为 .

【解析】本题考查菱形的性质,等边三角形的性质;能够判断出点P的运动轨迹,根据垂线段最短求最小值是解题的关键.由已知可以得到△ABC是等边三角形,点P的运动轨迹在△ABC的外接圆上,过点C作CE⊥AD与圆相交于点P,与AD相交于点E,此时CE PE最小,∵∠D=60°,AB=2√3,∴CE=2√3×√3/2=3.
变式2-3.如图,在菱形ABCD中,∠B=120°,AB=4,点E是BC的中点,点F在CD边上,点C关于EF的对称点为C′,连接EC′,FC′,当点F从C运动到点D的过程中,AC′长度的最大值与最小值的差为 .

【解析】先确定最大值:①当F与C重合时,C′与C重合,AC′=AC最大,作对角线求AC即可,可求得 AC′=AC=4√3;
②如图2因为C与C′关于EF对称,所以当点F从C运动到点D的过程中,C′在以E为圆心,以EC为半径的圆上运动,当点C′在AE上时,AC′最小,构建直角三角形利用勾股定理求AE和C′E的长,根据AC′=AE﹣C′E=2√7﹣2,最后计算最大值与最小值的差4√3﹣(2√7﹣2)=4√3﹣2√7 2,AC′长度的最大值与最小值的差为:4√3﹣2√7 2,故答案为:4√3﹣2√7 2.


例题3.已知菱形ABCD中,∠BAC=60°,AB=4,点E为AD的中点,如图,现将△ACD以点C为中心进行旋转,求BE的最大值和最小值。

【解析】我们先看旋转某个角度的图形,如下图,我们仍然可以类比对折时求最值的思路,先确定要求线段的两端点中,哪个是动点,其运动所在轨迹是否是圆,再由旋转找到定长,即圆的半径。当圆作出来时,最大值和最小值就都迎刃而解了。BE的最大值为4 2√3,最小值4-2√3.

例题3的动态分析
变式3.如图3,△ABC、△EFG均是边长为4的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M,当△EFG绕点D旋转时,则线段BM长的最小值和最大值分别是 和 .

【解析】取AC的中点O,连接AD、DG、BO、OM,如图,易证△DAG∽△DCF,则有∠DAG=∠DCF,从而可得A、D、C、M四点共圆,根据两点之间线段最短可得BO≤BM OM,即BM≥BO﹣OM,当M在线段BO与该圆的交点处时,线段BM最小,只需求出BO、OM的值,就可解决问题.故答案是:2√3﹣2;2√3 2.

方法总结:一箭穿心模型,通常为一条线段的最值问题,即动点的轨迹为圆或弧,利用点与圆的位置关系得到结果。
,




