平面直角坐标系中,点都是线与线相交而成。
在初中阶段,坐标系中的线主要有三类:直线(y=kx b,k≠0)、双曲线(y=k/x,k≠0)和抛物线(y=ax^2 bx c,a≠0 )。
比如二元一次方程组的解在坐标系中的几何意义是两条直线的交点。
理解这个基础模型对于分析类似的问题很有帮助。
再比如,二元一次方程组没有解的几何意义是两条直线平行(即直线的斜率k值相等)
基于这样的思路,可以把求解坐标点的问题转换为:线与线的交点。
这样把求点的坐标转换成先求解析式问题,再解方程组。
求三类线(直线、双曲线和抛物线)的解析式方法这里不赘述。

这道题看上去有些困难。
假设知道了OP的解析式(表现形式:二元一次方程),结合给定的抛物线解析式(表现形式:二元二次方程),联立后得到一个一元二次方程,问题便等到解决。
由于OP和AB相交,为使问题变得简洁一些,可过点A作OP的平行线AM,若求出AM的解析式,OP的解析式容易得到。(这种转换的思路需要平时积累)
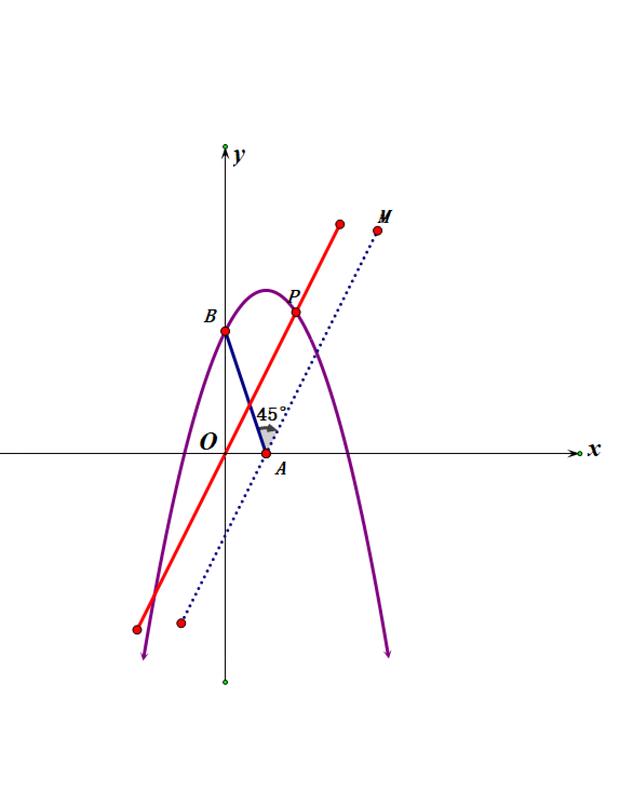
如何求AM的解析式呢?
由于点A已知,若能在AM上再找一个确定点,两点确定直线,问题也得到解决。
看见45°(或者30°、60°)最常见的方法是构造直角。
在平面直角坐标系中,天然的就和直角有关。
如下图所示,过点B作BD垂直AB交AM于点D
是不是看到熟悉的一线三垂直模型?
很容易把点D的坐标求出来。
通过简单代换,点D的坐标(3,4)。

从而求得AM的解析式为y=2x-2
从而OP的解析式为y=2x
知道了OP的解析式,与抛物线的解析式联立求得x=±√(3)
得到点P的坐标(√(3)、2√(3))
(舍去第三象限的坐标)
小结:求点的坐标,先求点所在线的解析式。通过几何模型寻找特殊点,从而求得解析式。
,




