纵观近几年全国各地中考题,圆的有关性质以及对于性质,概念的准确叙述等一般以填空题,选择题的形式考查并占有一定的分值;一般在10分-15分左右,圆的有关性质,如垂径定理,圆周角,切线的判定与性质等的运用一般以计算证明的形式考查;利用圆的知识与其他知识点如代数函数,方程等相结合作为中考压轴题将会占有非常重要的地位,另外与圆有关的实际应用题,阅读理解题,探索存在性问题仍是热门考题,请同学们注意.

类型1 结论探究问题
例1.(2018秋•江都区校级月考)已知:如图,△ABC内接于⊙O,AB为直径,点D是弧AC上的一点,连接AD、BD,AC交BD于点F,DE⊥AB于点E,交AC于点P,∠ABD=∠CBD=∠CAD.
(1)求证:PA=PD;
(2)判断AP与PF是否相等,并说明理由;
(3)当点C为半圆弧的中点,请写出BF与AD的关系式.并说明理由.
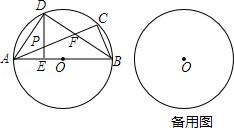
【分析】(1)由AB为⊙O的直径知∠ABD ∠BAD=90°、由DE⊥AB知∠BAD ∠ADE=90°,据此可得∠ABD=∠ADE,根据∠ABD=∠CAD得出∠CAD=∠ADE,从而得证;
(2)证∠EDF=∠DFP,得PA=PD=PF;
(3)延长AD、BC交于点H,先证△BDA≌△BDH得AD=DH=1/2AH,再证△ACH≌△BCF得BF=AH=2AD.
【解答】(1)∵AB为⊙O的直径,∴∠ADB=90°,即∠ABD ∠BAD=90°,
∵DE⊥AB,∴∠AED=90°,即∠BAD ∠ADE=90°,∴∠ABD=∠ADE,
∵∠ABD=∠CAD,∴∠CAD=∠ADE,∴PA=PD;
(2)∵∠DAF ∠AFD=90°,∠ADP ∠PDF=90°,且∠DAF=∠ADP,
∴∠AFD=∠PDF,∴PD=PF,
又∵PA=PD,∴PA=PF;
(3)如图,延长AD、BC交于点H,

则∠BDA=∠BDH=90°,
在△BDA和△BDH中,
∵

∴△BDA≌△BDH(ASA),∴AD=DH=1/2AH,
∵C为半圆弧的中点,∴AC=BC,
∵AB为⊙O的直径,∴∠ACB=∠ACH=90°,
在△ACH和△BCF中,
∵

∴△ACH≌△BCF(ASA),∴BF=AH=2AD.
【点评】本题主要考查圆的综合问题,解题的关键是掌握圆周角定理、等腰三角形的判定、全等三角形的判定与性质等知识点.

类型2 存在性问题
例2.(2018秋•泗阳县期中)如图,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0),(2,0),点M是AO中点,⊙A的半径为2.
(1)若△PAB是直角三角形,则点P的坐标为 .(直接写出结果)
(2)若PM⊥AB,则BP与⊙A有怎样的位置关系?为什么?
(3)若点E的坐标为(0,3),那么⊙A上是否存在一点P,使PE 1/2PB最小,如果存在,求出这个最小值,如果不存在,简要说明理由.

【分析】(1)依题意,分两种情形:①∠PAB=90°,②∠APB=90°分别求解即可解决问题;
(2)求出PA,PB的长,利用勾股定理的逆定理证明即可;
(3)如图3中,连接EM.由△PAM∽△BAP,推出PM/PB=PA/AB=1/2,推出PM=1/2PB,推出PE 1/2PB=PE PM,由PE PM≥EM,推出PE PM的最小值为线段EM的长.由此即可解决问题;
【解答】(1)设P(m,n),
①如图1,当∠PAB=90°时,
∵⊙A的半径为2,且A(﹣2,0),
∴点P1(﹣2,2),P2(﹣2,﹣2);
②如图2,当∠APB=90°,

∵A(﹣2,0),B(2,0),
∴PA^2=(m 2)^2 n^2=2^2①,
PB^2=(m﹣2)^2 n^2,AB^2=16,
由PA^2 PB^2=AB^2得4 (m﹣2)^2 n^2=16 ②
由①②得到:m=﹣1,n=±√3,
∴P(﹣1,√3)或(﹣1,﹣√3).
故答案为(﹣2,2)或(﹣2,﹣2)或(﹣1,√3)或(﹣1,﹣√3).
(2)如图2中,∵PM⊥AB,∴∠AMP=∠BMP=90°,
在Rt△APM中,∵∠PMA=90°,PA=2,AM=1,

∴PA^2 PB^2=4 12=16,
∵AB^2=16,∴PA^2 PB^2=AB^2,∴∠APB=90°,∴△PAB是直角三角形.
(3)如图3中,连接EM.
∵PA^2=4,AM•AB=4,∴PA^2=AM•AB,∴PA/AM=AB/PA,
∵∠PAM=∠BAP,∴△PAM∽△BAP,∴PM/PB=PA/AB=1/2,
∴PM=1/2PB,∴PE 1/2PB=PE PM,
∵PE PM≥EM,∴PE PM的最小值为线段EM的长,
∵E(0,3),∴OE=3,

【点评】本题属于属于圆综合题,考查了勾股定理以及逆定理,相似三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会利用分类讨论的思想思考问题,学会构造相似三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.

类型3 自定义问题
例3(2018•南通模拟)如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若弧CD的长为13π/4,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24 13√3,直接写出AP的长.

【分析】(1)利用平角求出∠APD=60°,即可得出结论;
(2)先求出∠COD=45°,进而判断出点D,P,E在同一条直线上,求出∠CED,即可得出结论;
(3)①当点P在半径OA上时,利用(2)的方法求出∠CFD=60°,∠COD=120°,利用三角函数求出CD,进而求出DF,再用勾股定理求出OH,即可求出OP即可得出结论;
②当点P在半径OB上时,同①方法求出BP=3,即可得出结论.
【解答】∠CPD是直径AB的“回旋角”,
理由:∵∠CPD=∠BPC=60°,
∴∠APD=180°﹣∠CPD﹣∠BPC=180°﹣60°﹣60°=60°,
∴∠BPC=∠APD,∴∠CPD是直径AB的“回旋角”;
(2)如图1,∵AB=26,∴OC=OD=OA=13,

∴n=45,∴∠COD=45°,
作CE⊥AB交⊙O于E,连接PE,∴∠BPC=∠OPE,
∵∠CPD为直径AB的“回旋角”,∴∠APD=∠BPC,∴∠OPE=∠APD,
∵∠APD ∠CPD ∠BPC=180°,∴∠OPE ∠CPD ∠BPC=180°,
∴点D,P,E三点共线,∴∠CED=1/2∠COD=22.5°,
∴∠OPE=90°﹣22.5°=67.5°,∴∠APD=∠BPC=67.5°,∴∠CPD=45°,
即:“回旋角”∠CPD的度数为45°,
(3)①当点P在半径OA上时,如图2,过点C作CF⊥AB交⊙O于F,连接PF,
∴PF=PC,同(2)的方法得,点D,P,F在同一条直线上,
∵直径AB的“回旋角”为120°,∴∠APD=∠BPC=30°,∴∠CPF=60°,
∴△PCF是等边三角形,∴∠CFD=60°,
连接OC,OD,∴∠COD=120°,
过点O作OG⊥CD于G,

∴PD PC=24,
∵PC=PF,∴PD PF=DF=24,
过O作OH⊥DF于H,
∴DH=1/2DF=12,
在Rt△OHD中,利用勾股定理可得OH=5,
在Rt△OHP中,∠OPH=30°,∴OP=10,∴AP=OA﹣OP=3;
②当点P在半径OB上时,同①的方法得,BP=3,∴AP=AB﹣BP=23,
即:满足条件的AP的长为3或23.
【点评】此题是圆的综合题,主要考查了垂径定理,三点共线,锐角三角函数,勾股定理,新定义,正确作出辅助线是解本题的关键.


类型4 研究性问题
例4.(2018秋•锡山区期中)(1)问题背景
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为弧BmC上一动点(不与B,C重合),求证: √2PA=PB PC.
请你根据图中所给的辅助线,给出作法并完成证明过程.
(2)类比迁移
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.

(3)拓展延伸
如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=4/3AC,AB⊥AC,垂足为A,则OC的最小值为_______.
【分析】(1)将△ACP绕点A顺时针旋转90°到△ABQ的位置,由旋转的性质可得:∠QBA=∠PCA,AP=AQ,PC=QB,根据圆的内接四边形的性质可证点Q,点B,点P共线,根据勾股定理可证√2AP=PQ=PC PB;
(2)连接OA,将△OAC绕点A顺时针旋转90°至△EAB,连接OB,OE,则可得EB=OC,AE=OA=3,∠EAB=∠OAC,根据勾股定理可求OE=3√2,根据三角形三边关系可得BE≥OE﹣OB=3√2﹣3 (当点B在OE上时,取等号),即可求OC的最小值;
(3)如图③构造相似三角形即可解决问题.作AQ⊥OA,使得AQ=4/3OA,连接OQ,BQ,OB.由△QAB∽OAC,推出BQ=4/3OC,当BQ最小时,OC最小.
【解答】(1)将△ACP绕点A顺时针旋转90°到△ABQ的位置.
证明如下:∵BC是直径,∴∠BAC=90°=∠BPC
∵AB=AC,∴∠ACB=∠ABC=45°
由旋转可得∠QBA=∠PCA,PA=AQ,PC=QB
∵∠PCA ∠PBA=180°,∴∠QBA ∠PBA=180°,∴Q,B,P三点共线
∴∠QAB ∠BAP=∠BAP ∠PAC=90°,∴QP2=AP2 AQ2=2AP2
∴QP=√2AP=QB BP=PC PB,∴√2AP=PC PB
(2)如图2:连接OA,将△OAC绕点A顺时针旋转90°至△EAB,连接OB,OE,

∵AB⊥AC, ∴∠BAC=90°
由旋转可得:EB=OC,AE=OA=3,∠EAB=∠OAC
∴∠EAB ∠BAO=∠BAO ∠OAC=90°,

∴OC最小值是3√2﹣3
(3)如图③中,作AQ⊥OA,使得AQ=4/3OA,连接OQ,BQ,OB.

∵∠QAO=∠BAC=90°,∠QAB=∠OAC,
∵QA/OA=AB/AC=4/3,∴△QAB∽△OAC,∴BQ=4/3OC,
当BQ最小时,OC最小,易知OA=3,AQ=4,OQ=5,BQ≥OQ﹣OB,
∴BQ≥2,∴BQ的最小值为2,∴OC的最小值为3/2
故答案为3/2.
【点评】本题考查圆综合题、全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理.三角形的三边关系等知识,解题的关键是学会利用旋转法添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.

总之,我们在圆问题中要领悟思想方法:遇到直径时,一般要引直径上的圆周角,将直径这一条件转化为直角的条件.遇到有切线时,一般要引过切点的半径,以便利用切线的性质定理;或连结过切点的弦,以便利用弦切角定理.遇到过圆外一点作圆的两条切线时,常常引这点到圆心的连线,以便利用切线长定理及其推论.求周长和面积要注意利用割补思想.圆柱和圆锥的侧面展开图是研究“化曲为直”的一条重要的思想方法.
针对近几年中考命题方向的预测,我们提出了复习的对策.
1. 打牢基础:准确理解与圆有关的概念及性质,理解弦、弧、圆心角与圆周角之间的关系; 会从点与圆,直线与圆关系中探索相应半径与距离的数量关系;会用垂径定理、切线长定理来证明一类与圆有关的的几何题;会利用圆内接四边形的性质、弧长与扇形面积公式,解决与圆柱,圆锥展开图有关的计算题并会借助分割和转化思想求阴影面积.
2.掌握方法:圆的复习不仅要抓住基础题目的基本方法,还要从典型问题的特殊方法着手强化训练,在解决问题的过程中不仅要善于掌握解题方法,而且要从中及时总结规律,为以后解题提供帮助.
3.关注应用:会利用圆的有关知识解决一些有关圆的实际应用题,动态题,探索题及阅读理解题等

我们在复习时要从学科整体意识和思想方法上着手,掌握圆的有关性质、与圆的有关的位置关系;注重通性通法,淡化特殊技巧方法.我们要认真研究试题解题过程中的思维方法,注意考查不同思维方法的试题的协调和匹配,数学思想方法,内容丰富,形式多样.在复习阶段应该对数学思想方法进行梳理总结,逐个认识它们的本质特征、思维程序和操作程序.使我们的数学理性思维能力得到较全面的提高,举一反三,以不变应万变.
真心真情真东西,讲究提供最新鲜最实用的考试素材,原创不易,期待你的关注留言分享等,2019我们共同进步。
,