问题:已知二维连续型随机变量(X,Y)的联合概率密度为f(x,y),讨论Z=g(X,Y)的密度函数 f_Z(z)。针对X与Y的四则运算,给出相应概率密度公式。
1.四则运算概率密度① Z=X±Y
此时,随机变量 Z 的概率密度为

或

当随机变量 X, Y 相互独立时, 有

或

对于加的情况,上述公式后两个即卷积公式。
② Z=X·Y
此时,随机变量 Z 的概率密度为:

或

当随机变量 X, Y 相互独立时, 有:

或

③ Z=X/Y
此时,随机变量 Z 的概率密度为:

当随机变量 X, Y 相互独立时, 有:
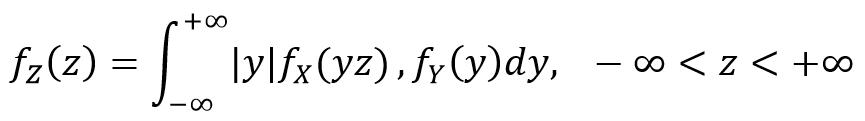
由于使密度函数非0的随机变量X, Y 取值范围不一定总是全体实数,上述公式中,积分限的变化就会比较复杂,通常积分限都是 z 的函数。以对 x 积分的公式为例,确定变量 x 积分限的具体做法如下。
第①步 由密度函数f(x,y)中y的范围确定x的范围。
设联合密度函数非0的平面区域为D:
a<x<b, c(x)<y<d(x)
从z=g(x,y)解得y=y(x,z), 代入上面不等式:
a<x<b, c(x)<y(x,z)<d(x)
再解上面第二个不等式得:
a<x<b, x_1(z)<x<x_2(z)
这一步将c(x)<y<d(x)变为x_1(z)<x<x_2(z)。
第②步 根据a<x<b, x_1(z)<x<x_2(z)的公共部分确定x的积分限。
注意到,积分限受z值的影响。这一步可用两种办法:
方法一:根据不同z值,在(一维)数轴上确定公共部分,即为x的积分区域。
方法二:在(二维)平面上,以z为横轴,x为纵轴画出区域:
a<x<b, x_1(z)<x<x_2(z)
根据z不同值确定x范围,即为x的积分区域。
03例子
例 设随机变量(X, Y)的概率密度为

分别求(1)Z=X Y, (2)Z=XY的概率密度。
解 (1)应用前述公式,采用对x积分。
第①步 先确定x的积分区域。联合密度函数非0区域D:
0<x<1, 0<y<1
从z=x y中解得y=z–x, 代入上面不等式得:
0<x<1, 0<z–x<1
再解上面第二个不等式得:
0<x<1, z–1<x<z
第②步 根据0<x<1, z–1<x<z的公共部分确定x的积分限。
注意到,积分限受z值的影响。这一步可用两种办法:
方法一:根据不同z值,在(一维)数轴上确定公共部分,即为x的积分区域。
当z≤0时,无公共部分无积分域,f_Z(z)=0;

当0<z≤1时,公共部分为0<x<z, 则:

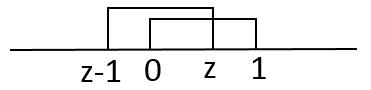
当1<z<2时,公共部分为z-1<x<1, 则:


当z≥2时,也无公共部分,f_Z(z)=0。

方法二:在(二维)平面上,以z为横轴,x为纵轴画出区域:
0<x<1, z-1<x<z

根据z的不同值确定x范围,即为x的积分区域。显然有:
当0<z≤1时,积分区间为0<x<z;
当1<z<2时,积分区间为z-1<x<1;
当z≤0或z≥2时,积分区间长度为0。
根据不同积分区域可得密度函数为:

(2)应用前述公式,采用对x积分。
第①步 先确定x的积分区域。联合密度函数非0区域D:
0<x<1, 0<y<1
从z=xy>0中解得y=z/x, 代入上面不等式:
0<x<1, 0<z/x<1
再解上面第二个不等式得:
0<x<1, x>z
第②步 根据0<x<1, x>z的公共部分确定x的积分限。
注意到,积分限受z值的影响。

当0<z<1时,积分区间为z<x<1,

当z≤0或z≥1时,无积分区间,f_Z(z)=0。
,




