geogebra描点法画函数图像（过定点画函数图像）

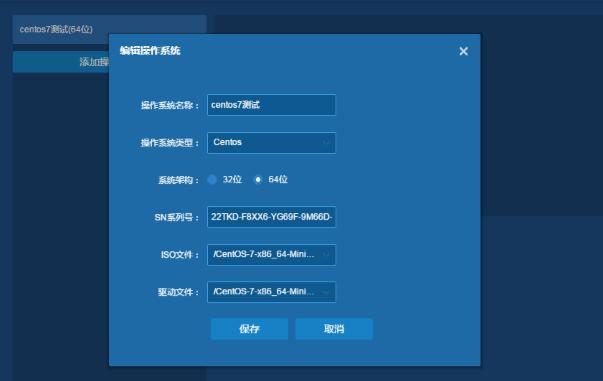
前言：轻松作图都是一二个指令的事。

1. 已知几个点，过点画函数图像
2. 绘制函数大致图像
3. 题目配以函数简图

多项式拟合( <点列>, <多项式次数> )

【举例】已有点A,B,C，过这三点作二次函数图像

【输入】多项式拟合({A, B, C})

【备注1】"多项式次数"不输入时，默认生成为次数比点的个数少一的多项式。

也就是，多项式拟合({A, B, C}) 等同于多项式拟合({A, B, C},2)

【备注2】“点列"即点的列表。在GeoGebra中，用花括号{ }表示列表。

快速形成一个列表的操作：

选中多个对象，拉进输入栏

总结：要生成n次函数，只需运用指令多项式拟合( <点列>)，而点应有 (n 1) 个。

题目配以函数简图

可做个简易坐标系工具，方便使用

请选择原点，分别输入：x最小、最大值，y最小、最大值

加了坐标系，就可以用在试卷上了。

简易坐标系工具的制作教程见置顶留言。

其他相关指令

指数拟合( <点列> )

对数拟合( <点列> )

正弦拟合( <点列> )

图中带颜色的文字为相应的指令，至于函数表达式可在代数区查看。

还有：

幂函数拟合( <第一象限点列> )

拟合曲线( <点列>, <函数> )

拟合直线X( <点列> )

等等

,