编者按
盼望着,盼望着,期末来了,考试的脚步近了……
为了表示对期末党的关爱,今天小编安排了动漫题材,希望大家都能顺利通过考试。
不考试&不看动漫的三元人士也不用失望,扒开本文二次元的伪装,您依然可以看到熟悉的硬核知识~
前几日,小编在取材(摸鱼)的时候,无意间竟然发现新一集《博人传:火影忍者新时代》的标题——

作为一名出生于上世纪的老二次元,笔者满怀期待地点开视频,然而……

这竟然就是第一场考试的全部内容……
(图片来源:iqiyi)
小编默默关上了视频,心中更是五味杂陈——是时候让这些年轻人感受真正的忍道啦!所以,这篇文章就是教大家如何科学地通过中忍选拔考试。
中忍选拔考试简介
中忍考试,顾名思义,是下忍(低级忍者)升为中忍(中级忍者)的考试,一年举行两次。综合《兵之书》、Narutopedia、Boruto Wiki等资料,可知虽然每届考试试题及形式可能会因为考官不同而有所差异,但基本的模式是相似的。本文将以《火影忍者》第一季漩涡鸣人首次参加考试为背景,为大家简单回顾中忍考试的基本情况。
考试内容:9道题 1道附加题,检验考生的侦察能力——允许作弊,但必须瞒过监考老师,被抓到5次被淘汰。
显而易见,有大量考生在第一轮笔试中就惨遭淘汰。所以要想在之后的考试中大展身手,最为关键的就是要通过第一场笔试的考验,这也是区分路人和主角的重要阶段。






考场上各显神通的忍者们
(图片来源:youku)
针对考生考试中表现的分析可知,有些考生获取答案的方式较为特殊,不太适宜大范围推广(譬如宁次、佐助利用血继限界这需要拼爹;又如牙、志乃需要特定“忍具”的协助携带宠物入考场)。
相比之下,我爱罗同学的手法(利用仿生学技术制造眼球)比较贴近现实,但获取的影像尺寸较小且清晰度不足(可能与制造眼球的材料是沙子有关)。因此我们接下来将探索如何才能获取清晰的试卷影像。图像处理的算法博大精深,包罗万象。这里针对我爱罗获取图像尺寸和清晰度的特点,主要介绍图像放大和图像增强算法。


上图:我爱罗用沙子制成仿生眼球
下图:我爱罗获取的试卷影像,并不十分清晰
(图片来源:youku)
“比更大还更大”——插值法
图像不清晰的首要原因是图像不够“大”。但是在日常生活中我们都会有类似的体验,位图在放大后质量会明显下降。因此不能简单地通过修改尺寸的方法来放大位图。为了保证位图放大之后的图像质量,需要我们在像素阵列中插入一定的值,保证放大后的阵列不至稀疏。
小知识:位图指的是使用像素阵列表示的图像。相对应地,基于数学方程的几何图元表示的图像被称为矢量图。换言之,矢量图是“算”出来的,所以放大之后质量不会下降。而位图是阵列“摆”出来的,放大将使得阵列变得稀疏,从而影响图片质量。

位图vs矢量图
一个简单的思路就是,选择距离所求数据点最近点的值,同时忽略其他相邻点,从而产生一个分段常数的内插值来作为所求数据点的值,即所谓最近邻插值法。该算法实现起来非常简单,但由于忽略了其他相邻数据点的信息,所以效果也略逊于其他算法。
另一个显而易见的思路是,假设相邻两个像素的值都位于这两个数值所确定的直线上,而这种方法也就是所谓的线性插值法。方法的思路十分简单,基本可以借助初中的数学知识来实现。

线性插值法
方法的思路十分简单,基本可以借助中学的数学知识来实现。已知两点(x,y)与(x,y)的具体值,求区间[x, y]内某一位置x对应的值y。假设x与y满足函数y=f(x),f(x)的表达式并不确定。如果两点的距离不远,我们不妨假设此时(x,y)与(x,y)满足直线方程的表达式,利用真·高中数学知识(直线方程两点式)可得

稍作处理

给出x3的值,就可以很容易地求出y3。
对于实际的二维图像,情况会稍微复杂一些,但本质上也是上面线性插值法的扩展,即所谓的双线性插值法。双线性插值法的核心思想是在两个方向分别进行一次线性插值。
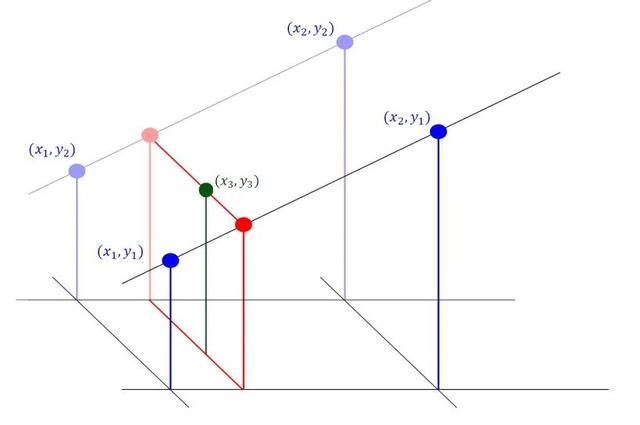
双线性插值法
下面的推导过程,学有余力的同学可以点开
点击展开
推导过程
假设图像Z可以表示为函数z=f(x, y)的集合,其中(x, y)代表某个像素的位置,z代表这个像素的色彩值。譬如已知(x,y),(x,y),(x,y)和(x,y)四个点,我们可以套用上面的方法求得区域内(x,y),也就实现了插值。具体而言,先考虑x方向的线性插值,有

然后考虑y方向

稍微处理一下,可以让公式更好看一点

当然,我们可以参考线性插值法的思路更进一步,利用非线性函数进行插值,以提高放大后图片的品质。例如前面提到的几种方法中,双三次插值的效果一般优于另外几种方法,一方面三次函数本身较其他几种函数更具优越性,另一方面双三次插值采集了插值点附近16个点的信息(多于二维最近邻、双线性的4个采样点和双二次的9个采样点),也就可以更好地体现图像的细节。

Jerry亲自示范如何在人群中运用插值算法
(图片来源:bilibili)
获得更多细节——图像增强
当然,对于很多图像来说,仅仅放大仍然不足以为我们提供足够的细节,这时候我们就需要通过其他算法以实现图像增强(如提高图像的对比度,突出图像的轮廓/锐化等)。

图片来源:qq
实现图像增强的算法有很多,需要根据具体的应用场景加以选择。此处根据我爱罗获得图像的特点,尝试增强图片的对比度。一般而言,一个图像的对比度不足,往往是由于图像像素强度(或者通俗点说,每个点颜色的深浅)过于集中导致的。处理的思路也非常简单粗暴,就是通过一定的变换,将原本集中的像素强度分散开来。理想状态下,变换后图像像素强度的概率密度呈均匀分布,而这也就是直方图均衡化算法的内在逻辑。

原图(左上)vs 直方图均衡化(左下)
图片来源:Wikipedia
右侧为对应图片的直方图(红)及累积分布函数。显然,直方图均衡化之后的图像变“亮”了许多,山上的树木变得清晰,山坡的纹理也得以显现。
下面的具体推导过程,学有余力的同学可以点开
点击展开
推导过程
具体而言,如果我们用代表原图像,设定图像为8位深度(图中每个像素颜色所占的二进制位位数),所以像素强度共有=2=256级。假设为像素强度出现的次数,为图像所有像素数。那么原图像归一化的概率分布直方图()

变换后图像的累积分布函数g写作

于是我们可以定义变换,= (),则有

这里不妨假设()与()分别为与对应的连续变量,且,∈[0,−1]。对于连续变量而言,变换同样成立=(),那么有

其中为的概率密度函数,相应地

为了简化问题,假设变换可微且可逆,显然有

即
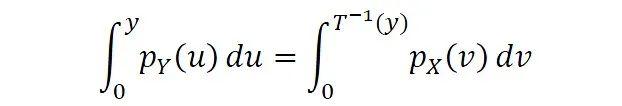
其中为的概率密度函数。运用复合函数求导法则,


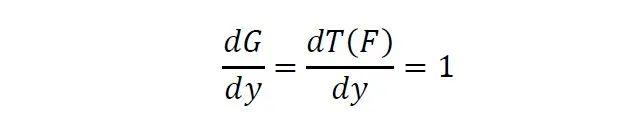
同时

所以

即我们期望得到的均匀分布的概率密度函数。换言之,变换就是我们的目标变换。
数值模拟——从理论到实践
上文粗略地介绍了几种算法的思路和基本原理,接下来,我们将理论应用于实战之中,借助python的OpenCV库来实现前述的各种算法。当然有兴趣的读者也可以尝试使用其他语言来实现(譬如Matlab就直接内置了函数interp1和interp2来处理一维和二维插值问题)。
首先我们来测试插值法。本文主要测试最近邻插值算法、线性插值算法和三次插值算法。考虑到手机端的呈现效果(不会吧,不会吧,不会真的有人用电脑刷微信公众号吧?)这里我们只选取了我爱罗视野中的部分信息,然后分别利用三种算法,长和宽都扩大为原来的15倍,效果如下



最近邻插值算法(左)、线性插值算法(中)和三次插值算法(右),右下角小图为原始图像
(点击图片放大看更清晰哦)
显然,经过最近邻插值算法放大的图像,边缘出现了明显的锯齿。而利用(双)线性插值和(双)三次插值算法处理的图像边缘比较平滑,没有出现明显的锯齿形状。
接下来,我们测试几种常见的图像增强算法。首先我们直接在原始图像上使用直方图均衡化算法,此时我们得到的图像如下:

直方图均衡化
显然,直方图均衡化的表现不够理想。主要原因在于一般的直方图均衡化算法使用从图像直方图导出的相同变换来变换所有像素。这对于像素值分布相似的图像较为有效,但对于纸卷这种部分内容(如字迹)明显比大部分图像更深暗的区域,这些区域反而无法得到充分的增强。当然要改善这种情况,一个思路就是利用前文的插值算法对图像进行预处理。

双三次插值预处理后的直方图均衡化
上图在使用直方图均衡化前,首先利用双三次插值算法处理原图像。利用插值算法使整张图的像素分布更为均匀。当然我们也可以使用限制对比度自适应直方图均衡化(CLAHE)算法,每个像素都根据像素周围图像的直方图进行变换,同时限制放大的程度,从而减少噪声也被放大的问题。

限制对比度自适应直方图均衡化
当然,除了上述提到的算法之外,读者朋友们也可以选择直接运用数理化知识,把题目解出来。
彩 蛋 时 间
话说我爱罗到底看到了哪一道题呢?


经过相关算法进行图像处理后得到的图像


“大人,时代变了!”
图片来源:youku、zhihu@无妄之神
转载内容仅代表作者观点
不代表中科院物理所立场
原标题:学习不好都看不懂动漫了——论如何科学地通过忍者考试
来源:科学大院
编辑:just_iu
,




