本节将中学里的集合和映射做了些适当的加深. 首先回顾下常用的记号:
∅: “空集”
∀: “任意”
∃: “存在”
∄: “不存在”
∃!: “存在且唯一”
A ⇒ B: “A 推出 B”
A ⇔ B: “A 和 B 等价”
A := B: “A 由 B 定义”
n!: “自然数 n 的阶乘, 即 1 × 2 × 3 · · · × n”
(2n)!!: “偶数 2n 的双阶乘, 即 2 × 4 × 6 · · · × 2n = 2nn!”
(2n 1)!!: “奇数 2n 1 的双阶乘, 即 1 × 3 × 5 · · · × (2n 1)”
组合数 n!/k!(n − k)!, 0 ≤ k ≤ n”
[x]: “实数 x 的整数部分”
<x> : “实数 x 的小数部分, 即 x-[x]
给定一个集合 A, 其幂集 (power set) 定义为
2^A := {A 的所有子集}.
根据定义显然有 A ∈ 2^A, ∅ ∈ 2^A, {x} ∈ 2^A 对所有 x ∈ A 都成立, 故 2^A 必不是空集. 又比
如易证,
2^∅ = {∅}, 2^{∅} = {∅, {∅}}
和
2 ^{♣,♢} = {∅, {♣}, {♦}, {♣, ♦}} .
给定集合 A 和 B, 定义如下几个集合运算:
A 和 B 的并 (union):
A ∪ B := {x : x ∈ A 或 x ∈ B}.
A 和 B 的交 (intersection):
A ∩ B := {x : x ∈ A 且 x ∈ B}.
B 在 A 中的差 (difffference of B in A):
A \ B := {x ∈ A : x 不属于 B}
A 和 B 的对称差 (symmetric difffference):
A4 B := (A \ B) ∪ (B \ A).
假设 A 是全集 I 的子集, 则 A 在 I 中的差称为A 的余集 (complement of A) 并记为
C_I (A) ≡ A^C := I \ A.
在高中时期, 我们知道如何用文氏图 (Venn diagrams)(这是英国数学家、逻辑学家和哲学家John Venn在 1880 年的论文《On the diagrammatic and mechanical representation of propositions and reasonings, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 5, 10(1880), no. 59, 1–18》中引入的, 但是类似的想法可追溯到Christian Weise在 1712 年的书《Nucleus Logicoe Wiesinoe》和Leonhard Euler在 1768 年的信《Letters to a German Princess》中. Venn当时称之为“欧拉圈”, 而“文氏图”的叫法是之后出现在Clarence Irving Lewis在他的著作《A Survey of Symbolic logic》中.)来表示集合间的关系. 请诸位用文氏图来表示集合 A 和 B 在全集 I 中的对称差.
假设 A, B, C 是全集 I 中的集合, 根据定义立即得到
(i) 交换律 (commutativity): A ∪ B = B ∪ A, A ∩ B = B ∩ A.
(ii) 结合律 (associativity): A ∪ (B ∪ C) = (A ∪ B) ∪ C, A ∩ (B ∩ C) = (A ∩ B) ∩ C.
(iii) 分配律(distributivity): A∪(B∩C) = (A∪B)∩(A∪C), A∩(B∪C) = (A∩B)∪(A∩C).
(iv) A ⊆ B ⇐⇒ A ∪ B = B ⇐⇒ A ∩ B = A.
(v) De Morgan 法则 (De Morgan’s law): A \ (B ∪ C) = (A \ B)∩(A \ C), A \ (B ∩ C) =
(A \ B) ∪ (A \ C).
(vi) A ∩ (B \ C) = (A ∩ B) \ (A ∩ C), A ∪ (B \ C) ⊇ (A ∪ B) \ (A ∪ C).
(vii) A = (A ∩ B) ∪ (A \ B).
到此为止我们回顾了中学时期关于集合的基本性质. 接下里我们介绍集合的公理化
定义. 初学者可直接跳过接下来关于 ZFC 集合公理化部分, 从第 1.5.1 小节开始.
什么是集合? 集合是如何定义的? 这两个最基本、最朴素的问题回答起来是非常
困难的. 本节开头我们试图粗略的给出集合的“公理化定义”(主要参考文献:
R. 戈德门特 著 (王耀东 译, 张小萍 校): 代数学教程, 法兰西数学精品译丛, 高等教育出版社, 2013 年.
Jech, Thomas. Set theory, The Third Millennium Edition, Revised and Expanded, Springer, 2006.
Bourbaki, N. Theory of sets, Springer, 2004.
李文威 著: 代数学方法 (第一卷), 现代数学基础, 67.1, 高等教育出版社, 2019). 著名的 Russell 佯谬
(Russell’s paradox) 是指考虑所有集合构成的集合 U, 并构造子集 S := {x ∈ U|x /∈ x}.
此时我们要问:
S 是否属于 S?
假如 S 不属于 S, 则根据 S 的定义必有 S ∈ S, 产生矛盾; 假如 S ∈ S, 则根据 S 的定义必有
S 不属于 S, 产生矛盾. 因此 S 不是集合, 从而 U, 集合的集合, 不是集合. 换句话说, 如下的概
括公理不成立:
(10) 概括模式公理 (axiom schema of comprehension) (不成立): 如果 P 是关于集合的性
质, 并以 P(x) 表示 x 满足性质 P, 则存在集合 Y = {x|P(x)}.
常用的集合公理化是 ZF 公理化集合论 (Zermelo-Fraenkel axiomatic set theory), 而通常
所谓的 ZFC 是表示带选择公理的 ZF 理论 (the theory of ZF with the axiom of choice).
ZFC 共有 9 个公理. 在详细解释上述公理之前, 我们首先引入集合论中的形式语言.
二元谓语 (binary predicate): 等号 (equality) =, 从属关系 (membership relation) ∈.
连词 (connectives): ∧, ∨, ¬, →, ↔,
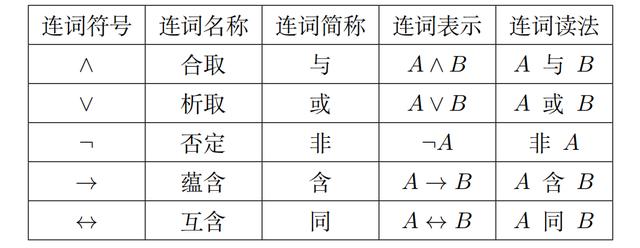
连词
量词 (quantififiers): ∀, ∃.
这样集合论中的表达式 (formulas) 是由原子公式 (atomic formulas)
x ∈ y, x = y
通过连词和量词所构筑而成的. 如果 ϕ(x, p_1, · · · , p_n) 是表达式, 则称
C := {x|ϕ(x, p_1, · · · , p_n)}
为类 (class), 即 x ∈ C 当且仅当 ϕ(x, p_1, · · · , p_n). 两个类
C = {x|ϕ(x, p_1, · · · , p_n)}, D = {x|ψ(x, q_1, · · · , q_m)}
是相等的, C = D, 如果
∀x(ϕ(x, p_1, · · · , p_n) ↔ ψ(x, q_1, · · · , q_m)).
万有类 (universal class) 或宇宙 (universe) 是所有集合的类,
U := {x|x = x}
定义类的包含关系 (inclusion)(此时称 C 是 D 的子类 (subclass)):
C ⊆ D 当且仅当 ∀x(x ∈ C → x ∈ D)
和如下类运算:
C ∩ D := {x|(x ∈ C) ∧ (x ∈ D)},
C ∪ D := {x|(x ∈ C) ∨ (x ∈ D)},
C \ D := {x|(x ∈ C) ∧ (x /∈ D)},
UC:= {x|∃S∈C(x∈S)}.
每个 (满足 ZF C 公理) 集合S 都可以看成类{x|x∈S}. 当然也存在不是集合的类(比如在 Russell 佯谬中定义的 S), 称为真类 (proper class).
(ZF C1) 外延公理 (axiom of extensionality): 如果 X 和 Y 有相同的元素, 则 X = Y .
∀u(u ∈ X ↔ u ∈ Y ) → X = Y.
这意味着集合是被它的元素所决定的.
(ZF C2) 配对公理 (axiom of pairing): 对任意 a 和 b, 存在 {a, b} 只包含 a 和 b.
∀a∀b∃c∀x(x ∈ c ↔ (x = a) ∨ (x = b)).
根据外延公理得到上述 c 是唯一的, 从而我们可定义对 (pair)
{a, b} := 唯一的 c 满足 ∀x(x ∈ c ↔ (x = a) ∨ (x = b)).
单点集 (singleton) {a} 定义为 {a} = {a, a}.
(ZF C3) 分离模式公理 (axiom schema of separation): 令 ϕ(u, p1, · · · , pn) 是表达式. 对任意X 和任意 p_1, · · · , p_n 存在 Y = {u ∈ X|ϕ(u, p_1, · · · , p_n)}.
∀X∀p_1 · · · ∀p_n∃Y ∀u(u ∈ Y ↔ u ∈ X ∧ ψ(u, p_1, · · · , p_n)).
对类 C = {u|ϕ(u, p_1, · · · , p_n)}, 我们得到
∀X∃Y (C ∩ X = Y ).
这就意味着类 C 和集合的交是集合. 作为推论我们可以定义
X ∩ Y := {u ∈ X|u ∈ Y }, X \ Y := {u ∈ X|u 不属于 Y }.
同样空类 (empty class)
∅ := {u ∈ X|u 不等于u}
是集合, 称为空集 (empty set). 其中 X 是任意集合. 注意到这个定义的前提是这样的 X 至少存在一个, 这可由无穷公理保证. 空集 ∅ 的定义和 X 的选取无关, 这一点可由外延公理得到. 两个集合 X, Y 称为互不相交的 (disjoint) 如果 X ∩ Y = ∅.
(ZF C4) 并集公理 (axiom of union): 对任何 X, 存在 X 的集合 Y = U X.
∀X∃Y ∀u(u ∈ Y ↔ ∃z((z ∈ X) ∧ (u ∈ z))).
这样我们可以定义
X ∪ Y := ∪{X, Y }, X ∪ Y ∪ Z := (X ∪ Y ) ∪ Z, 等等.
同样可定义
{a, b, c} := {a, b} ∪ {c}, {a_1, · · · , a_n} := {a_1} ∪ · · · ∪ {a_n}.
最后得到 X 和 Y 的对称差: X ^Y := (X \ Y ) ∪ (Y \ X).
(ZF C5) 幂集公理 (axiom of power set): 对任何 X, 存在 X 的集合 2^X.
∀X∃Y ∀u(u ∈ Y ↔ u ⊆ X).
这里集合 U 称为X 的子集 (subset of X), 记作 U ⊂ X, 如果
∀z(z ∈ U ↔ z ∈ X).
若 U ⊆ X 且 U不等于 X, 称 U 是X 的真子集 (proper subset of X). X 的所有子集构成
2X := {u|u ⊆ X},
称为X 的幂集 (power set of X).
对任何 X 和 Y 定义它们的乘积 (product) 为
X × Y := {(x, y)|(x ∈ X) ∧ (y ∈ Y )}
其中 (x, y) := {{x}, {x, y}}. 因为
X × Y ⊆ 2^{2^{X∪Y}},
因此 X × Y 是集合.
(ZF C6) 无穷公理 (axiom of infifinity): 存在无穷集.
∃S ((∅ ∈ S) ∧ ((∀x ∈ S)x ∪ {x} ∈ S)).
上述用形式语言描述的无穷公理告诉我们
∅ ∈ S ⇒ ∅ ∪ {∅} ∈ S ⇒ {∅} ∈ S ⇒ {∅} ∪ {{∅}} ∈ S
⇒ {{∅}} ∈ S⇒ {{∅}} ∪ {{{∅}}} ∈ S ⇒ {{{∅}}} ∈ S
特别地,
∅ ∈ S, {∅} ∈ S, {∅, {∅}} ∈ S,
从而得到无穷集合
{∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}, · · · }.
(ZF C7) 替换模式公理 (axiom schema of replacement): 如果类 F 是函数, 则对任意集合 X
存在集合 Y = F(X) = {F(x)|x ∈ X}.
类 F 称为函数 (function) (注意: 这里的函数定义和通常函数的定义是不一样的!) 如
果 F 是某个乘积 C × D 的子集, 且 (c, d) ∈ F 和 (c, d′) ∈ F 推出 d = d′. 此时定义
定义域 (domain) 和值域 (range) 分别为
Dom(F) := {c|存在 d(c, d) ∈ F}, Ran(F) := {d|存在 c(c, d) ∈ F}.
注意到 Dom(F) 和 Ran(F) 都是集合, 这是因为
Dom(F) ⊆ UUF, Ran(F) ⊆ UUF.
替换模式公理告诉我们如果类 F 是函数且定义域 Dom(F) 是集合, 则值域 Ran(F)
也是集合.
(ZF C8) 正则公理 (axiom of regularity): 每个非空集合都有一个 ∈-极小元素.
∀S (S不等于 ∅ → (∃x ∈ S)S ∩ X = ∅).
作为直接推论得到, 不存在无穷链· · · ∈x_2 ∈ x_1 ∈x_0 , 否则的话考察集合 S =
{x_0, x_1, x_2, · · · }. 因此不存在集合 x 满足 x ∈ x.
(ZF C9) 选择公理 (axiom of choice): 每个非空集合构成的集族都存在选择函数.
如果 S 是集族且 ∅ 不属于 S, S 的选择函数 (choice function) 是指映射 f : S → US 满足
条件
f(x) ∈ x, x ∈ S.
即从每个集合 x ∈ S 中都可以选择出一个元素 f(x) ∈ x.
到此为止, 我们简略介绍了 ZFC 集合公理化. 详细阐述可参考
Jech, Thomas. Set theory, The Third Millennium Edition, Revised and Expanded, Springer,
2006.
Bourbaki, N. Theory of sets, Springer, 2004.
这两本专著. 从李文威著作
李文威 著: 代数学方法 (第一卷), 现代数学基础, 67.1, 高等教育出版社, 2019.
的第一章中也可获得不少有趣的收获, 比如 Grothendieck 宇宙.
从现在开始, 我们采用朴素的、通常意义下的集合理论, 即中学时期所讲的集合理论.
,