在生活中很多常见的物品都是长方体,例如各种包装纸盒等等。
无盖长方体是怎样制作出来的呢?请看下图:

从左往右看,是制作示意图;从右往左看,是降维打击。
在降维打击中,蕴含着重要的数学思想——转化思想。即将复杂的立体几何问题转化为简单的平面几何问题来研究。
现在问题来了:
七年级学生Shirley买了一张漂亮的卡纸,并裁剪为边长20厘米的正方形。她问我,数学要上综合实践课,怎样利用这张正方形卡纸,制作一个容积最大的无盖长方体?
这是一个很棒的问题!如果不是课本提出来的,而是学生自由思考后主动提出来的,那就更好了。
现在我们开始探索之旅。
首先,动手制作一个长方体。在卡纸上画图,再剪去四个角的小正方形,翻折四条边并粘好固定。于是,长方体做好了。

还有没有别的制作方法?有,请看下图:

图二和图三制作的长方体容积一样大,但图二更麻烦,所以我们选择图三更方便。
现在我们来探究长方体容积的变化规律。

用代数式表达长方体的容积:
V=(a-2b)(a-2b)b
从公式看出,a是定值,b是影响容积的重要变量。
我们列表计算长方体的容积:把a=20,b分别在1~10取值计算,结果如下表。

再制作图形,把数据可视化:
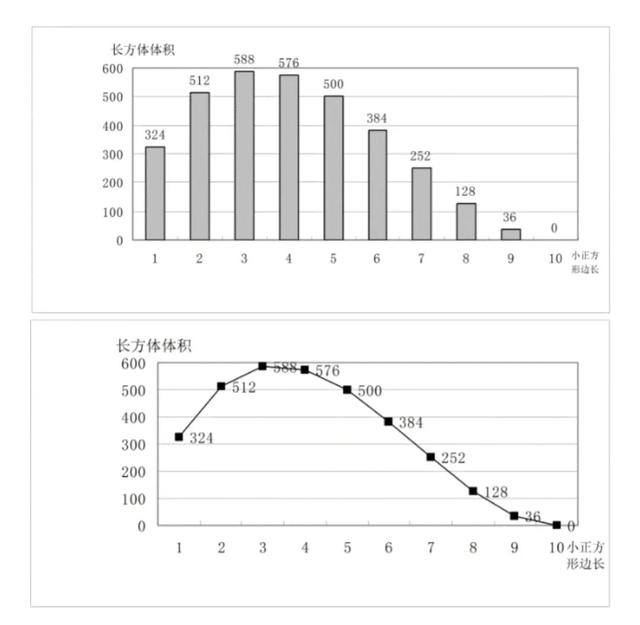
条形统计图和折线统计图
现在对b和V的关系有初步的感性认识了。小正方形边长b不能太大,也不能太小,要找到合适的值才能使容积最大。
我们用代数方法来探究长方体的容积变化规律。
要求出最大值,要运用两个代数定理:
[定理1]若n个正数x₁、x₂、x₃...xₙ的和为定值,当它们彼此相等时,其乘积最大。即 若x₁ x₂ x₃ ... xₙ=k(k为常数)
则当x₁=x₂=x₃=...=xₙ时,函数 y=x₁x₂x₃...xₙ达最大值。
[定理2]若n个正数x₁、x₂、x₃...xₙ的乘积为定值,当它们彼此相等时,其和最小。即 若x₁x₂x₃...xₙ=k(k为常数)
则当x₁=x₂=x₃=...=xₙ时,
函数 y=x₁ x₂ x₃ ... xₙ达最小值。
这两个定理很容易理解。你想,一个数,例如12,把它分为相等的两个数,当然乘积最大。6×6当然大于4×8。正方形面积总是大于相同周长的长方形面积。
这两个定理也不要求七年级学生证明,只有明白数学的严谨由数学家的辛勤工作保证,前人已经证明过了,我们感谢数学家即可。
有了武器,我们开始用代数方法寻求容积V的最大值。
把代数式变形,
(a-2b)(a-2b)b
=1/4(a-2b)(a-2b)4b
我们注意到上式的红色字体部分展开后等于2a是一个常数,就可以运用定理1了。若(a-2b) (a-2b) 4b为定值时,则当(a-2b)=(a-2b)=4b时,
(a-2b)(a-2b)4b达最大值。
由(a-2b)=4b可得a=6b,
即b=a/6时,长方体容积最大。
1999年,李政道先生以外籍院士的身份,为院士科普系列图书写了一本小册子《对称和不对称》。书中谈到了物理学家定律很有趣,引用如下:
物理学家第一定律:没有实验物理学家,理论物理学家就要漂浮不定。
要理解物理学家的定律,你完全不必知道任何物理学定律。
物理学家第二定律。没有理论物理学家,实验物理学家就会犹豫不决。
引自:今日头条文章:李政道《对称与不对称》书摘笔记15:物理学的发现和物理学家的定律
现在,有了理论的指导,我们就可以像实验物理学家一样,重新设计实验方案。
现在我们把a设定为30,b分别取值4.99999和5以及5.00001,然后计算长方体的容积,结果如下:
b=4.99999,a-2b=20.00002,
V=1999.99 999 999
继续,
b=5,a-2b=20,
V=2000
继续,
b=5.00001,a-2b=19.99998
V=1999.9999 9999
实验结果表明,实验物理学家证明了理论物理学家的模型是正确的。
宋玉在《登徒子好色赋》中说:东家之子,增之一分则太长,减之一分则太短 ;著粉则太白,施朱则太赤......
我们刚才求的最大值可谓妙到毫巅,比东家之子有过之而无不及。
继续思考,如果不要求底面是正方形,长方体的容积还能不能更大?百度文档的网友经过认真思考,提出了本问题的最佳答案:
如果没有底面必须是正方形的限制,还有一个最佳设计方案:

图七
如图所示,黄色底面是a·a/2的长方形,红色部分是较长的高,蓝色部分是较短的高。
按a=30来计算长方体的容积,
V=30×15×5=2250
值得称奇的是,原材料的利用率达到100%,没有产生边角料的浪费。
总结:底面是正方形的方案比较容易制作。当b=a/6时,长方体容积达最大值:

上图是正方形底面的长方体的最大容积和相应的表面积计算。
结论:如果要求底面是正方形,那么最佳方案是b=a/6;
如果不要求底面是正方形,那么最佳方案是图七。
a是作为原材料的大正方形的边长,b是长方体(无盖)的高。
Shirley还问了最后一个问题,如何构造三阶幻方?
南宋数学家杨辉总结出一套方法,不过对七年级学生不合适。
推荐阅读头条文章:
https://m.toutiao.com/is/8N1jeK3/?=数学的神韵by李尚志(国家级数学名师) - 今日头条
第四章节:幻方的设计——以简驭繁,
讲得非常好,读后受益匪浅。
科学尚未普及,媒体还需努力。感谢阅读,再见。
,