文章对很多的家长是很大的帮助的,每天都为大家带来更多的教育知识,考点知识,每天不定时分享,希望各位家长及时阅读、收藏、转发,评论交流心得
如孩子遇到问题可在下方评论区留言交流

平行四边形作为特殊的四边形,一直是中考试题中的主角。尤其是在综合了函数知识后动态研究它的存在性问题,对学生分析问题和解决问题的要求较高。
此类题目主要考查平行四边形的判定与性质、函数解析式的确定与性质,考查识图作图、运算求解、数学表达等能力,数形结合、分类讨论、函数与方程等数学思想。学生在处理问题的时候,往往不能正确分类,导致漏解。
此外,在解题时一般需要添设辅助线,借助
平行四边形的对角线性质,来探究平行四边形的存在性问题就是一个很好的途径。
平行四边形对角线互相平分的坐标探究

即平行四边形每条对角线上两个顶点的横坐标之和相等,纵坐标之和也相等。根据这个结论就可简洁地解决平面直角坐标系中平行四边形存在性问题。
如图 3,A、B、C 是平面上不在同一直线上的三个点。① 画出以 A、B、C 为顶点的平行四边形;② 若 A、B、C 三点的坐标分别为(- 1,5)、( -5,1)、(2,2),请写出这个平行四边形第四个顶点 D 的坐标。

此题是解决平行四边形存在性问题的基础题,由于有三个点已经确定,在作图时,一般会分别选择 AB、AC、BC 为对角线来进行画图,但这样的前提是要有三个定点。然而很多灵活复杂的此类问题却往往只有两个定点,所以可以把其中的以 BC 为对角线转换成以 AD 为对角线,这样就可以以不变应万变了,只要取定已知点比如 A,然后按 AB、AC、AD 分别为对角线来进行分类。这样能够比较明确的得到所有情况,而且可以避免遗漏。
如图 4,以 AB 为对角线的平行四边形 AD1BC;以AC 为对角线的平行四边形 ABCD2;以 BC 为对角线的平行四边形 ABD3C.设 D1 坐标为(x,y).
在平行四边形AD1BC中,对角线 AB与 CD1互相平分,也就是 AB 的中点与CD 1 的中点重合,A、B、C三点的坐标分别为( -1,5)、 ( -5,1)、 (2,2), 所以可得方程组:
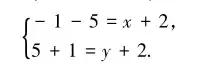
解得D点的三种情况坐标。
在解答平面直角坐标系中平行四边形存在性问题时,首先可将四个点的坐标表示出来,然后利用与其中一点有关的三条线段分别为对角线进行分类,最后根据对角线互相平分时中点重合,构造方程组进行求解。
巧用对角线探究平行四边形的存在性
利用对角线进行分类讨论,再利用对角线互相平分构造等量关系,是否也能处理比较复杂的存在性问题呢?举例说明。



巧用对角线探究平行四边形的适度拓展
在一些问题中,还常常会要求学生讨论菱形、矩形的存在性。此时我们可在上述基础上增加相应条件,如增加两条对角线互相垂直、邻边相等得到菱形,增加邻边互相垂直、对角线相等得到矩形,利用点坐标求得相应线段的长度从而求解。事实上利用坐标求解的思路还适用于等腰三角形、直角三角形、圆的存在性问题。有时,我们甚至还可以通过构造平面直角坐标系来求解。
已知正方形ABCD,点E 是BC 上一点,以 AE 为边作正方形 AEFG.
(1) 连接 GD,求证:△ADG ≌ △ABE;
(2) 连接FC,求证:∠FCN = 45°;
(3) 请问在 AB 边上是否存在一点Q,使得四边形DQEF是平行四边形?若存在,请证明;若不存在,请说明理由。

(3) 如图,以B为坐标原点,BA 为 y 轴,BC 为 x 轴,设 BE = a,BC = 1,BQ = b, 过 F 作 FH ⊥ x 轴,可得 △ABE ≌ △EFH,所以 E 点坐标(a,0),F点坐标(1 a,a),D点坐标(1,1),Q点坐标(0,b),又因为四边形 DQEF 是平行四边形。只能 DE,QF为对角线。



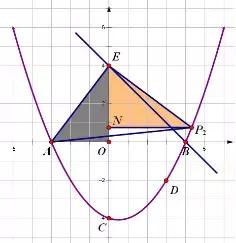

一般利用对角线互相平分的四边形是平行四边形,利用两点的中点公式进行求解,当四边形只有1个顶点是动点时,我们可以利用已知的三点求出平行四边形的第4个顶点,然后看这个点的坐标是否符合题意;当有两个点是动点时,先设其中的一个动点的坐标为(a,b)在根据这3点的坐标求出第4点的坐标,再把这个点代入它所在直线或者抛物线的解析式中,求出a,b的值。
其次我们把图形进行分割,利用三角形全等来解决,方法见 动态问题中的正方形。
再次我们可以一组对边平行且相等的四边形是平行四边形,这时候需要用到两点之间的距离公式(可以利用勾股定理计算),因为已知的两点所在的直线解析式可以求出,再利用平行线的k值相等,设平行于已知直线的解析式为y=kx b,分别联立方程求出两个交点的坐标(用含有b的式子表示),再计算这两个交点之间的距离,使这个距离等于已知两点之间的距离。
需要注意的是,任意两点的连线可能是四边形的一条边或者对角线,我们需要分情况来讨论。
思考
已知抛物线y=ax² bx c的对称轴为x=3/2,与x轴的交点A的坐标为(﹣1,0),与y轴的交点为C(0,-4)
(1)求抛物线的解析式;
(2)M在抛物线上,N在抛物线的对称轴上,是否存在点M、N,使A、C、M、N四点组成的四边形是平行四边形,若存在,求出M、N的坐标;若不存在,请说明理由。


温馨提示:如果你孩子在各科成绩都不是很理想,贪玩,主动、约束能力差,不要一直埋怨孩子,掌握一套好的学习方法,提高孩子的记忆力与理解力,一切都事半功倍。孩子还会不爱学习吗?咨询我回复001,免费获取更多学习资料解析答案以及最强大脑记忆方法,让孩子轻轻松松学习,快快乐乐升学!
,




