导数的结果应该是严格的特定的0/0——如欧拉所言(1运算)
(今天开始发表关于求导数运算的结果的文章。现在微积分在高中已经讲授。从运算的角度看,不是非常困难。困难在于最后的求极限。为了让更多的人容易理解,我的文章讲解得比较详细。文章很长,所以也分为若干部分。建议耐心一些,慢慢看,不要着急。)
1 求导数的运算——从代数运算转化为微积分运算
求导数的运算是微积分的基本运算之一,而且属于入门的运算。这个运算并不十分困难,而且已经公式化了。现在我国的高中阶段已经讲授微积分。但是在求导数的运算中需要应用目前的极限概念,在这个时候就会发现其中有问题。从下面的例子可以清楚地看出这一点。
希望读者至少具备高中的数学知识。但是为方便读者阅读,这里的阐述将尽量详细一些。先假定函数y=f(x)是连续可导的,则可经过变化、求差、作比、求极限这四个步骤求出导数。为了更明确地讨论,举个实际函数y=ax^2(a≠0,a为常量而且a﹥0)(符号“^”表示乘方,这里表示y等于a乘以x的二次方。)为例,并给予讨论(请参考图1(图形过几天再发。请耐心。))。如果不结合例子,则讨论容易变成“空对空”,问题暴露的不鲜明。(现在大学里讲微积分的时候,常常先讲极限,包括极限的概念、运算,以及无穷小量、无穷大量和连续性等等。讲了一大堆,然后才讲到利用极限求导数。这当然有一定的道理,可是也有问题:由于有比较大的间隔,结果却使其中存在的本来非常明显的矛盾变得模糊了。)
上面提到了几个概念。其中函数是一个非常基本的概念,在中学数学中已经学过了。这里简单的重复一下。如果有两个变量(即在某个运算过程中可以变化的数量),其中的一个变量发生变化时,如果另外一个变量也随着第一个变量的变化而变化,则我们就把第一个变量称为自变量,而把第二个变量称为函数(亦称为因变量)(比较清楚地这样定义函数的第一个人是欧拉[1])。更多的变量的情况可以类似的定义。通常在数学的一元函数中经常使用字母x表示自变量,而用y表示函数,用式子y=f(x)表示y是x的函数。“连续”这个概念在中学也介绍过,但是它比我们想象的要复杂。以后再说。至于“可导”的含义,将在求出下面的例子中的导数之后再说明。
①变化 让自变量由x 变化到x1 (这是以后运算的基础和出发点),于是函数y也变化为y1
y1=f(x1); ∵ y=ax^2 (1.1)
∴y1=ax1^2 (注意:下标表示不了。y1的1是y的下标。x1含义相同。建议参考下面的图片。) (1.2)
②求差 求出两个差值,就是变化后的自变量x1和变化前的自变量x的差,以及相应的函数y1和y的差。我们分别用Δx和Δy表示这两个差(Δ是希腊字母,念“德尔塔”,在数学中通常用来表示两个数量的差):
Δx=x1-x (1.3)
Δy=f(x1)-f(x)=ax1^2-ax^2
=a(x Δx)^2-ax^2
=2ax Δx a Δx^2 (1.4)
③作比 即算出上面的函数的差与自变量的差的商值Δy/Δx(马克思称之为预备导函数,即在一个区间里建立了新关系,但现在是近似的关系,不是准确的关系):

(1.5)
以上3步运算看起来都是代数运算,因为都是有限量的运算,比较容易理解和接受。但是从微积分的角度看,这3个步骤属于预备步骤,所以马克思称(1.5)式的结果为“预备导函数”。[2]
④求极限,即x1→x或Δx→0,于是得出了y的导数(也常常称为“微商”),通常用y’表示(或用dy/dx表示,它们可以通用,但是有时候它们又各有各的用处)(下面的运算中出现了极限的符号“lim”,念“利眯特”,是拉丁文limis[3]的缩写。另外符号“→”也表示极限):
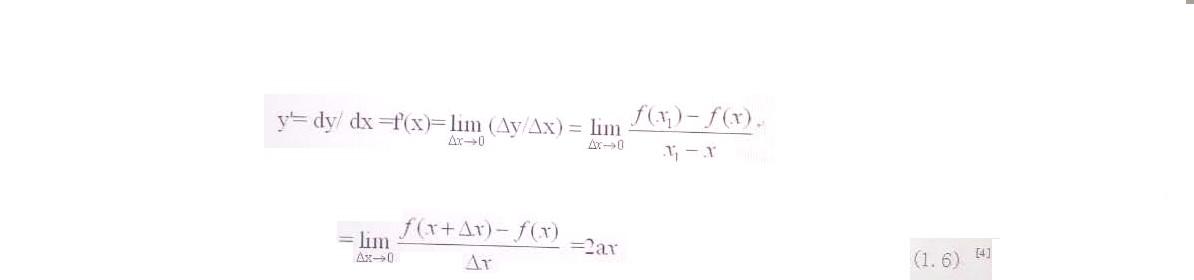
(1.6) [4]
至此导数已经求出:y'=2ax,运算结束。显然,上面的(1.6)式的含义是:函数y=ax^2的导数y'等于当Δx→0的时候Δy/Δx的极限值。
需要强调指出的是,导数是基于原来的函数所求出的一种新关系。它有具体的含义:它是函数的变化量与自变量的变化量的比值,也就是函数值的变化数量对自变量的变化数量的变化率。函数的导数还有具体的几何含义:原函数在这一点的切线的斜率。在本节3中我们将有进一步的说明。
上面的运算并不困难。但是如何理解求导运算,特别是第四步求极限的运算呢?Δx→0的含义究竟是什么呢?这是难点所在。
应该特别指出,这一步运算是关键性的:由于Δx→0,从而原来的代数运算即“预备”运算已经转化成为微积分的运算。微积分运算的特点是:利用极限才能进行到底。只囿于代数学则不可能彻底说清楚微积分的运算。而前面三步的运算与代数运算只是看起来几乎没有什么差别。但是这三步是预备运算,已经不是纯粹的代数运算。在第四步则彻底告别代数运算,走入了自己的“领地”。
(这里我们开始接触到微积分的一个核心概念:极限。以后如果有机会,会详细说明极限。)
我们首先说明“可导”的含义。在上面的运算中,如果在x变化的时候,不论变大还是变小,即无论Δx﹥0还是Δx﹤0,经过相应的运算之后所得出的导数的数值(注意:必须包括符号)都是相同的,则称这个函数在这一点处是“可导”的。反之,如果在这两种情况下,求出的导数是不同的,则这个函数在这一点就是不可导的,或者只是单侧可导的。很显然,函数y=ax^2是处处可导的,因为从上面的具体运算中,我们容易看出,在函数y=ax^2的任一点处求导数时,无论Δx﹥0还是Δx﹤0,我们所得出的导数都是相同的(2ax)。
这里非常关键的是:求出的结果是2ax,而a Δx那一项已经完全消失了。这个结果实质上已经否定了现行的极限定义,因为现行的极限定义的基本点是:…略。(见后续文章。)
注释
1 欧拉《无穷分析引论》[M]山西教育出版社1997年1-6。欧拉《微分学引论》(英文版)即《Foundations of Differential Calculus 》Euler;Translated by John D.Blahton ©2000 Springer-Verlag, New York, Inc.ⅵ。
2 马克思《数学手稿》北京大学《数学手稿》编译组编译人民出版社1975年7月第1版4,5。
3 据《维基百科》,见http://zh.wikipedia.org/wiki/极限。
4 这一段参考了周述岐《微积分基本原理》修订本,中国人民大学出版社 1989年3月第二版103—104。不同的教科书中的论述大同小异。
,




