图的生成树和最小生成树的概念
在一个连通图G中,如果取它的全部顶点和一部分边构成一个子图G′,即:
V(G’)=V(G)和E(G’)ÍE(G)
若边集E(G’)中的边既能够把图中的所有顶点连通而又不形成回路,则称子图G’是原图G的一棵生成树(Spanning Tree)。
下面简单说明一下既包含连通图G中的全部n个顶点又没有回路的子图G’(即生成树)必含有n-1条边。要构造子图G’,首先从图G中任取一个顶点加入G’中,此时G’中只有一个顶点,假定具有一个顶点的图是连通的,以后每向G’中加入一个顶点,都要加入以该顶点为一个端点,以已连通的顶点之中的一个顶点为另一个端点的一条边,这样既连通了该顶点又不会产生回路,进行n-1次后,就向G’中加入了n-1个顶点和n-1条边,使得G’中的n个顶点既连通又不产生回路。
在图G的一棵生成树G’中,若再增加一条边,就会出现一条回路。这是因为此边的两个端点已连通,再加入此边后,这两个端点间有两条路径,因此就形成了一条回路,子图G’也就不再是生成树了。同样,若从生成树G’中删去一条边,就使得G’变为非连通图。这是因为此边的两个端点是靠此边唯一连通的,删除此边后,必定使这两个端点分属于两个相互独立的连通分量中,使G’变成了具有两个独立连通分量的非连通图。
连通图和它的生成树
在这三棵生成树中,图7-11(b)所示的树是从图中顶点v0出发利用深度优先搜索遍历得到的,被称之为深度优先生成树;图7-11(c)所示的树是从顶点v0出发利用广度优先搜索遍历得到的,被称之为广度优先生成树;图7-11(d)所示的树是任意一棵生成树。当然图7-11(a)的生成树远不止这几种,还可以画出其他许多种。
对于一个连通网(即连通带权图,假定每条边上的权均为大于零的实数)来说,生成树不同,每棵树的权(即树中所有边上的权值总和)也可能不同。图7-12(a)就是一个连通网,图7-12(b)、(c)、(d)是它的三棵生成树,每棵树的权都不同,分别为57、53和38。具有最小权的生成树称为图的最小生成树(Minimum Spanning Tree)。通过后面将要介绍的构造最小生成树的算法可知,图7-12(d)是图7-12(a)的最小生成树。
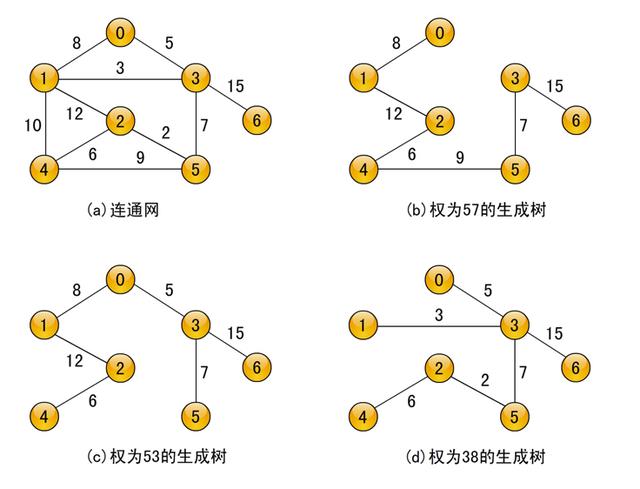
连通网和它的生成树
求图的最小生成树很有实际意义。例如,若一个连通网表示城市之间的通讯系统,网的顶点代表城市,网的边代表城市之间架设通讯线路的造价,各城市之间的距离不同,地理条件不同,其造价也不同,即边上的权不同,现在要求既要连通所有城市、又要使总造价最低,这就是一个求图的最小生成树的问题。
求图的最小生成树的算法主要有两个:一是普里姆(Prim)算法。另一是克鲁斯卡尔(Kruskal)算法。
图的生成树不唯一。因为同一个图可以有不同的生成树,只要能够连通所有顶点又不产生回路的任何子图都是它的生成树,如深度优先生成树、广度优先生成树等。
,




