三角形内角和等于180度,这是学生小学就已经知道了的知识点,可是初中为什么还要去学习?去研究?其关键点不是让孩子去知道三角形内角和等于180度,而在于学生在求证的过程中学会借助平行线的“移角”功能,将三角形内角和问题转化为平角问题或者两平行直线下的同旁内角问题,这是本节课的核心问题。
小学已经探究学习了三角形的内角和,但是我们仅仅是通过拼角为平角,或者量三角形三个内角并求和得到的,不管是拼还是量这都是肉眼所见下的平角以及测量下的和为180度。这都是有误差的,在数学学习里也是不严谨的,即使拼了量了一万个十万个百万个三角形,也只是代表这一部分满足,所以我们需要证明。
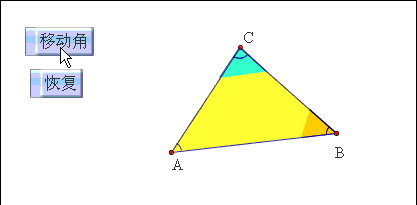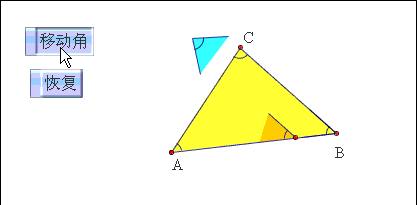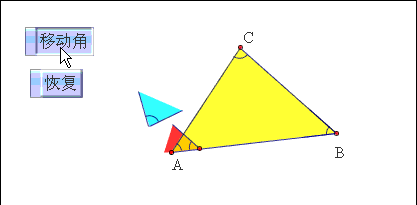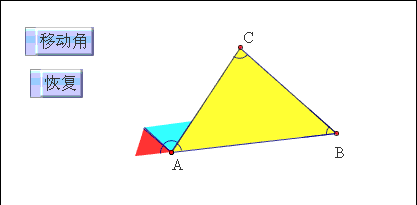
方法一:将三角形内角和问题转化为两条平行线下同旁内角问题。
已知:△ABC的三个内角是∠A,∠B,∠C.求证:∠A ∠B ∠C=180º.

证明:过点C作CD∥BA,则∠1=∠A∵CD∥BA∴∠1 ∠ACB ∠B=180°∴∠A ∠ACB ∠B=180°

方法二:将三角形内角和问题转化为平角问题。




当然证明三角形内角和的方法还有很多,但只要掌握了其核心的转化思想,其他的方法不需要知道也可。
欢迎留言讨论,共同进步。
,