【几何求值】
————————————————————
求线段的数量关系与位置关系是初中阶段常考的内容之一,那如何在纷繁复杂的题目中找到求线段长度的突破口呢。下面小编为大家整理了初中阶段常用求线段长度的方法。前四种是纯粹初中阶段的知识,后两种方法应用到高一的公式。由于中考中使用高中阶段知识解题并不算错误(应用错误则肯定不得分),因此特别普及一下。
【典型例题】
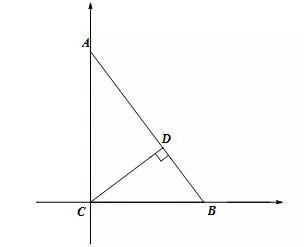
如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,CD为斜边AB上的高,求CD的长.

图1
【解析】
【方法一】等面积法——用不同方式表示同一三角形的面积
解:∵∠C=90°,AC=4,BC=3,∴AB=5.
又∵CD为斜边AB上的高,∴S△ABC=AC·BC=AB·CD,
∴4×3=5CD,CD=2.4.
【方法二】勾股定理——构造直角三角形,用勾股定理建立方程
解:∵∠C=90°,AC=4,BC=3,∴AB=5.
设BD=x,则AD=5-x.
又∵CD为斜边AB上的高,
∴在Rt△ADC与Rt△BDC中,
CD^2=AC^2-AD^2=BC^2-BD^2,
即4^2-(5-x)^2=3^2-x^2,x=2.4.∴CD=2.4.
【方法三】相似——根据边角关系发现相似三角形的模型
解:∵∠C=90°,AC=4,BC=3,∴AB=5,∠A+∠B=90°.
又∵CD为斜边AB上的高,∴∠BDC=∠ADC=∠C=90°.
∴∠A+∠ACD=90°.∴∠B=∠ACD.
∴△ABC∽△ACD.∴AB:AC=BC:CD,即5:4=3:CD,∴CD=2.4.
【方法四】锐角三角函数——遇直角,优先考虑三角函数与勾股
解:∵∠C=90°,AC=4,BC=3,∴AB=5.
又∵CD为斜边AB上的高,∴∠BDC=∠C=90°.
∴sin B=CD:BC=AC:AB,即CD:3=4:5.∴CD=2.4.
【方法五】两点之间的距离公式——勾股定理的推广,不超纲,选填直接用
如图2,以点C为坐标原点,CA,CB所在直线分别为x轴,y轴,建立平面直角坐标系.
则C(0,0),A(0,4),B(3,0).

【备注】两点间的距离公式:
A(x1,y1),B(x2,y2)
AB=√(x1-x2)² (y1-y2)²

【方法六】点到直线的距离公式——结合垂直的斜率关系
设直线AB的解析式为y=kx+4,代入B(3,0),得0=3k+4,k=-.


图2
【备注】两直线平行:k1=k2;两直线垂直:k1·k2=-1.
点到直线的距离公式:
点A(x′,y′),直线l:y=kx b,则
点A到直线l的距离为:d=|kx′-y′ b|/√(1 k²)

即:把y=kx b移项变成kx-y b=0,把点A的横纵坐标代入左边,得kx′-y′ b并取绝对值,再除以(1 k²)的算术平方根
怎么样?有收获吗?希望这些方法可以帮你找到解题的突破口,快速解决难题!
【举一反三】

你会几种解法呢?
,




