专注于Java领域优质技术号,欢迎关注来自:小旋锋
CAP定理是分布系统中的一个基本定理,它指出任何分布系统最多可以具有以下三个属性中的两个。
- 一致性 (Consistency)
- 可用性 (Availability)
- 分区容错性 (Partition tolerance)
本文将以图解的形式简明地对 Gilbert and Lynch's specification and proof of the CAP Theorem (CAP定理的规范和证明) 进行概括总结
什么是 CAP 定理?CAP定理指出分布式系统不可能同时具有一致性、可用性和分区容错性。听起来很简单,但一致性、可用性、分区容错性到底是什么意思呢?确切地来说分布式系统又意味着什么呢?
在本文中,我们将介绍一个简单的分布式系统,并对分布式系统的可用性、一致性和分区容错性进行诠释。有关分布式系统和这三个属性的正式描述,请参阅 Gilbert 和 Lynch 的论文。
分布式系统
让我们来考虑一个非常简单的分布式系统,它由两台服务器G1和G2组成;这两台服务器都存储了同一个变量v,v的初始值为v0;G1和G2互相之间能够通信,并且也能与外部的客户端通信;我们的分布式系统的架构图如下图所示:
一个简单的分布式系统
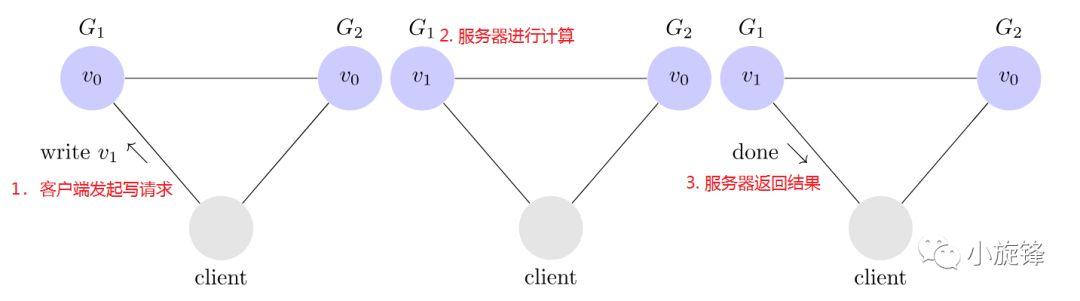
客户端可以向任何服务器发出读写请求。服务器当接收到请求之后,将根据请求执行一些计算,然后把请求结果返回给客户端。譬如,下图是一个写请求的例子:
客户端发起写请求
接着,下图是一个读请求的例子
客户端发起读请求
现在我们的分布式系统建立起来了,下面我们就来回顾一下分布式系统的可用性、一致性以及分区容错性的含义。
一致性 (Consistency)
Gilbert 和 Lynch 在论文中的描述是:
any read operation that begins after a write operation completes must return that value, or the result of a later write operation也就是说,在一个一致性的系统中,客户端向任何服务器发起一个写请求,将一个值写入服务器并得到响应,那么之后向任何服务器发起读请求,都必须读取到这个值(或者更加新的值)。
下图是一个不一致的分布式系统的例子:
不一致的分布式系统
客户端向G1发起写请求,将v的值更新为v1且得到G1的确认响应;当向G2发起读v的请求时,读取到的却是旧的值v0,与期待的v1不一致。
下图一致的分布式系统的例子:
一致的分布式系统
在这个系统中,G1在将确认响应返回给客户端之前,会先把v的新值复制给G2,这样,当客户端从G2读取v的值时就能读取到最新的值v1
可用性 (Availability)
Gilbert 和 Lynch 在论文中的描述是:
every request received by a non-failing node in the system must result in a response也就是说,在一个可用的分布式系统中,客户端向其中一个服务器发起一个请求且该服务器未崩溃,那么这个服务器最终必须响应客户端的请求。
分区容错性 (Partition tolerance)
Gilbert 和 Lynch 在论文中的描述是:
the network will be allowed to lose arbitrarily many messages sent from one node to another也就是说服务器G1和G2之间互相发送的任意消息都可能丢失。如果所有的消息都丢失了,那么我们的系统就变成了下图这样:
网络分区
为了满足分区容错性,我们的系统在任意的网络分区情况下都必须正常的工作。
CAP定理的证明
现在我们已经了解了一致性、可用性和分区容错性的概念,我们可以来证明一个系统不能同时满足这三种属性了。
假设存在一个同时满足这三个属性的系统,我们第一件要做的就是让系统发生网络分区,就像下图的情况一样:
网络分区
客户端向G1发起写请求,将v的值更新为v1,因为系统是可用的,所以G1必须响应客户端的请求,但是由于网络是分区的,G1无法将其数据复制到G2
由于网络分区导致不一致
接着,客户端向G2发起读v的请求,再一次因为系统是可用的,所以G2必须响应客户端的请求,又由于网络是分区的,G2无法从G1更新v的值,所以G2返回给客户端的是旧的值v0
由于网络分区导致不一致
客户端发起写请求将G1上v的值修改为v1之后,从G2上读取到的值仍然是v0,这违背了一致性。
总结我们假设了存在一个满足一致性、可用性、分区容错性的分布式系统,但是我们展示了在一些情况下,系统表现出不一致的行为,因此证明不存在这样一个系统
对于一个分布式系统来说,P 是一个基本要求,CAP 三者中,只能根据系统要求在 C 和 A 两者之间做权衡,并且要想尽办法提升 P
,