八年级数学中,全等三角形的判定是中考中要求最高的等级,掌握全等三角形的判定,学会证明两个三角形的全等,然后利用全等三角形的性质进行判定对应边相等,对应角相等。而证明三角形全等的方法很多,需要同学们根据给定的条件,灵活的选择合适的判定方法,并且能够综合的运用本章的知识,进行题目的解答。首先我们来看第一个判定定理,边边边定理,掌握边边边定理的注意事项,学会在在题目中挖掘隐含条件,最终解出问题。

边边边定理的判定方法是:三边分别相等的两个三角形全等,简写成“边边边”或“(SSS)”。这里需要注意的是:(1)、要证明两个三角形全等,应设法确定这两个三角形的三条边对应相等。(2)、书写格式上需要注意:在列举两个三角形全等的条件时,把三个条件按顺序排列,并用大括号将它们括起来。(3)、含有公共边的两个三角形,只要满足除公共边外的两个边对应相等,再加上图中隐含的公共边,由“SSS”就可以得到两个三角形全等,以及类似的条件也可以得到两个三角形全等。

例题1:点E、F在AC上,BF=DE,AB=CD,AE=CF。求证:△ABF≌△CDE.

【解析】:由题目可知,题干中都是边边的关系,优先考虑边边边定理。因为AE=CF,所以AE EF=CF EF,所以AF=CE.所以在△ABF和△CDE中,AB=CD,BF=DE,AF=CE,所以△ABF≌△CDE.在本题中,就存在隐含条件EF为公共部分,经过边长之间的运算,得到两条边的关系。
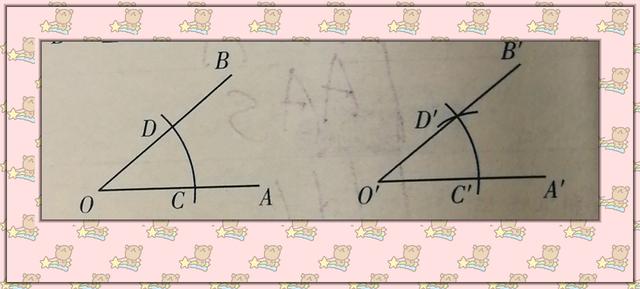
通过学习了解,判定两个三角形全等至少需要三个条件,证全等时应注意充分挖掘题中隐含条件:公共边或有公共部分的边通过线段的和与基来转化成对应边相等作为全等的条件,有时根据问题的需要,可以通过添加适当的辅助线构造全等三角形,需要注意的是,辅助线要用虚线画。而做一个角等于已知角,也是依据的边边边定理,作图的时候一定要注意保留作图痕迹。希望同学们不要畏惧几何类的证明题,将每一个定理和知识点掌握扎实,逐渐运用到综合题目中,几何题你会发现,并不是想象的那么难!加油。
,




