二叉树查找完整代码（一文彻底掌握二叉查找树）

树在数据结构中是重中之重，尤其以各类二叉树为学习的难点。现在希望通过写一个关于二叉树的专题系列。在学习与总结的同时更加深入的了解掌握二叉树，让我们开始吧！！！

定义

二叉查找树（Binary Search Tree），又称二叉排序树（Binary Sort Tree），亦称二叉搜索树。多种叫法，反正都是一个意思，这些叫法的由来主要是由它的性质决定的。

二叉树具有以下性质：

1. 一棵空树，或者是具有下列性质的二叉树

2. 若左子树不空，则左子树上所有结点的值均小于它的根结点的值

3. 若右子树不空，则右子树上所有结点的值均大于它的根结点的值

4.左、右子树也分别为二叉排序树

5. 没有键值相等的结点

二叉树的概念非常好理解，如下图所示就是一棵二叉查找树：

二叉树查找完整代码（一文彻底掌握二叉查找树）(1)

二叉查找树的操作

查找节点

1. 若比较关键字与根节点的大小，相等则成功返回

2. 若小于根节点，递归左子树

3. 若大于根节点，递归右子树

4. 若子树为空，查找不成功。

插入节点

1. 比较关键字与根节点的大小，相等则表示已存在，成功返回

2. 若小于根节点，递归左子树

3. 若大于根节点，递归右子树

4. 若子树为空，作为节点的子节点，返回

删除节点

二叉排序树删去一个结点，分三种情况讨论,先贴张图方便理解:

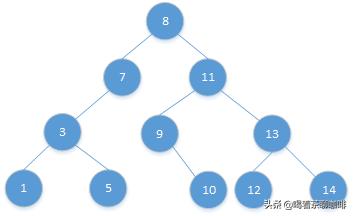
二叉树查找完整代码（一文彻底掌握二叉查找树）(2)

1. 删除的节点为叶子节点，直接删除，不会对树的结构有影响，如上图删除1，5，10，12，14

2. 删除的节点只有左子树或右子树，将节点的左子树或右子树作为父节点的左子树或右子树，删掉节点。如上图的删除节点7，将节点3作为8的左子树。删除节点9，则将10作为11的左子树

3. 删除的节点有左子树和右子树。找到右子树的最小节点，替换要删除的节点的位置。

第1，2种情况比较好理解，就不再赘述了，但第3种情况怎么理解呢？为方便讲解，把图标下颜色

二叉树查找完整代码（一文彻底掌握二叉查找树）(3)

假设要删除一个节点11，其左右子树为DL（绿色部分）、DR（黄色部分）。

即从树上把节点11摘除，同时将DL、DR两棵子树融合成一棵树DLR，挂到D原来的父节点上。

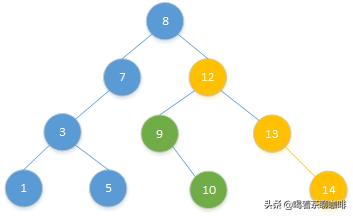
我们知道，二叉树的任意节点的左子树上的所有节点均小于其右子树上的所有节点。那么我们只要找到右子树上的最小的节点（该例子中为节点12），那么该节点必然小于右子树DR上所有其它节点，同时大于左子树DL上的所有节点，假设这个节点是M。

把左子树作为M的左子树，把右子树除去M然后作为M的右子树，这时产生的新的树必然满足二叉搜索树的定义。再把M替换原来D的位置，删除完成，结果如下图。

二叉树查找完整代码（一文彻底掌握二叉查找树）(4)

最后附上相关代码：

public class Tree { private Node root; public void insert(int value) { root = insert(root, value); } private Node insert(Node x, int value) { if (x == null) {// 首次插入 return new Node(value); } int xVal = x.value; if (value < xVal) { x.left = insert(x.left, value); } else if (value > xVal) { x.right = insert(x.right, value); } else { // do nothing } return x; } private class Node { private int value; private Node left, right; public Node(int value) { this.value = value; left = right = null; } } public Node select(int value) { return select(root, value);// work when BST is empty } private Node select(Node x, int value) { if (x == null) return null; int xVal = x.value; if (value < xVal) return select(x.left, value); else if (value > xVal) return select(x.right, value); else return x; } public void delete(int value) { root = delete(root, value); } private Node delete(Node x, int value) { if (x == null) return null; int xVal = x.value; if (value < xVal) x.left = delete(x.left, value);// 左子树 else if (value > xVal) x.right = delete(x.right, value);// 右子树 else { if (x.right == null) return x.left; if (x.left == null) return x.right; Node temp = x;// 要被删除的节点 x = min(temp.right);// 右子树的最小节点 x.right = deleteMin(temp.right);// 删除最小节点，同时返回右子树 x.left = temp.left;// 原来的左子树 } return x; } private Node min(Node x) { if (x.left == null) return x; return min(x.left); } private Node deleteMin(Node x) { if (x.left == null) return x.right; x.left = deleteMin(x.left); return x; } }

效率

对该二叉树的节点进行查找发现深度为1的节点的查找次数为1，深度为2的查找次数为2，深度为n的节点的查找次数为n，因此其平均查找次数为 (1 2 2 3 3 3) / 6 = 2.3次

二叉查找树可以任意地构造，同样是1,2,3,4,5,6这六个数字，也可以按照下图的方式来构造：

二叉树查找完整代码（一文彻底掌握二叉查找树）(5)