平移、旋转和翻折是几何变换中的三种基本变换。所谓几何变换就是根据确定的法则,对给定的图形(或其一部分)施行某种位置变化,然后在新的图形中分析有关图形之间的关系.这类试题的特点是:结论开放,注重考查学生的猜想、探索能力;便于与其它知识相联系,解题灵活多变,能够考察学生分析问题和解决问题的能力.在这一理念的引导下,纵观近几年全国各地的中考加大了这方面的考察力度,特别是2016年中考,这一部分的分值比前两年大幅度提高。
为帮助广大考生把握好这部分的知识,我分专题讲解这部分知识,今天来讲解旋转:
一、旋转的定义
在平面内,将一个图形绕一个定点沿某个方向转动一定的角度,这样的图形变换称为旋转,这个定点叫旋转中心,转动的角度叫旋转角.
旋转变换不改变图形的形状和大小.通过旋转,图形上的每一点都绕旋转中心沿相同的方向转动同样大小的角度.旋转变换前后的图形有下列性质:
(1)对应点到旋转中心的距离相等;


三、旋转的具体题目
(一)正三角形类型
在正ΔABC中,P为ΔABC内一点,将ΔABP绕A点按逆时针方向旋转600,使得AB与AC重合。经过这样旋转变化,将图(1-1-a)中的PA、PB、PC三条线段集中于图(1-1-b)中的一个ΔP'CP中,此时ΔP'AP也为正三角形。

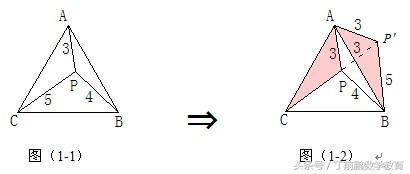
例1. 如图:(1-1):设P是等边ΔABC内的一点,PA=3, PB=4,PC=5,∠APB的度数是________.
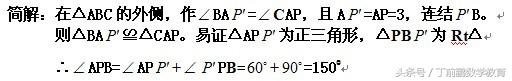
(二)正方形类型
在正方形ABCD中,P为正方形ABCD内一点,将ΔABP绕B点按顺时针方向旋转900,使得BA与BC重合。经过旋转变化,将图(2-1-a)中的PA、PB、PC三条线段集中于图(2-1-b)中的ΔCPP'中,此时ΔBPP'为等腰直角三角形。

例2. 如图(2-1):P是正方形ABCD内一点,点P到正方形的三个顶点A、B、C的距离分别为PA=1,PB=2,PC=3。求此正方形ABCD面积。

(三)等腰直角三角形类型
在等腰直角三角形ΔABC中,∠C=Rt∠, P为ΔABC内一点,将ΔAPC绕C点按逆时针方向旋转900,使得AC与BC重合。经过这样旋转变化,在图(3-1-b)中的一个ΔP'CP为等腰直角三角形。

例3.如图,在ΔABC中,∠ACB =900,BC=AC,P为ΔABC内一点,且PA=3,PB=1,PC=2。求∠BPC的度数。


总结:旋转是几何变换中的基本变换,它一般先对给定的图形或其中一部分,通过旋转,改变位置后得新组合,然后在新的图形中分析有关图形之间的关系,进而揭示条件与结论之间的内在联系,找出证题途径。
更过精彩内容,请关注数学教育 mathedu01
,




