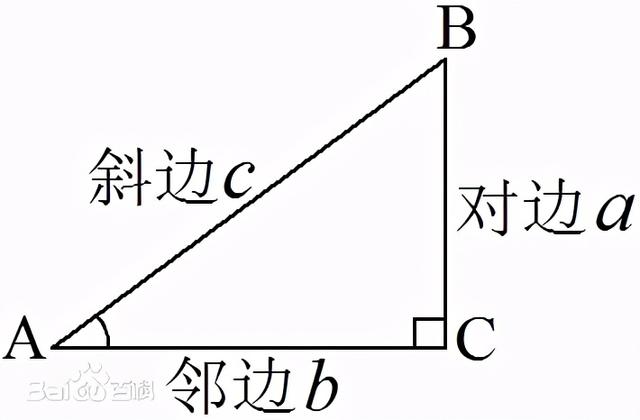
在直角三角形中,当平面上的三点A、B、C的连线,AB、AC、BC,构成一个直角三角形,其中∠ABC为直角。对∠ABC而言,对边(opposite)、斜边(hypotenuse)、邻边(adjacent),则存在以下关系:

|
基本函数 |
英文 |
缩写 |
表达式 |
语言描述 |
|
正弦函数 |
sine |
sin |
∠A的对边比斜边 | |
|
余弦函数 |
cosine |
cos |
|
∠A的邻边比斜边 |
|
正切函数 |
tangent |
tan |
|
∠A的对边比邻边 |
|
余切函数 |
cotangent |
cot |
|
∠A的邻边比对边 |
|
正割函数 |
secant |
sec |
|
∠A的斜边比邻边 |
|
余割函数 |
cosecant |
csc |
|
∠A的斜边比对边 |
矩阵的三角函数计算显然不能从上述三角函数的初等数学中的定义推导出来,因此我们需要借助于三角函数的高等数学中的定义。

高等数学中三角函数采用无穷级数方式进行定义:
其中自变量是实数或复数。

今天,我们这里假定自变量是一个阶方块矩阵,记为,则:
矩阵三角函数恒等式- ,与对应

先求二阶单位矩阵的正弦值:
,即

同理可以求得

,也即:
不难验证。

同样,我们也可以直接计算:

计算到前三十项


也就是说

所以,我们完全有理由相信,对任意矩阵,有恒等式
(请有兴趣的网友证明)
这个公式与三角函数恒等式完美对应。
- 求
根据指数为矩阵的指数函数是个什么鬼?,我们知道:
|
... |
... |
所以

所以,
所以,
由于,所以可以推导出一个有趣的级数恒等式:。

- ,与对应
令,用GeoGebra验证该恒等式成立:
改变方阵的值,二倍角三角函数恒等式都成立。这里我们只是采用了归纳法,演绎方法证明留给其他感兴趣的学者。
很遗憾,不成立。另外,已验证成立的其他恒等式:

- ,与对应;
- ,与对应,其中,是的逆矩阵,是对应的单位矩阵。
- ,与对应;
- ,与对应;
- ,,与三角函数的诱导公式对应;
- ,与对应;

本文将三角函数的定义域从实数域推广到矩阵,发现原三角函数很多性质在矩阵域仍然成立。
我不知道矩阵的三角函数的物理意义,更不明白其现实的潜在的使用价值,但这不是数学以及数学研究者的思索职责,因为数学是纯粹形而上的东西,尽管它常常被用于解决形而下的物理世界的问题。
本文只是在这些方面做了一个初步的探索,留下大量理论研究的空间。

2021年6月13日于安徽郎溪
,




