样本均值与总体均值的含义是不相同的。一般来说,我们想要获悉的是总体均值,但实际上,我们只能计算得到样本均值,然后用它来估计总体均值。我们使用置信区间,尝试用它用来评价“使用样本均值估计总体均值”的精确程度。
置信区间如果你想要估计国内女性的平均身高,你可能会这样做:调研10名女性的身高为样本,并估计:样本的均值接近于总体均值。让我们用程序模拟一下整个过程。

只是简单地获得样本均值没有太大意义,因为我们并不知道用它来估计总体均值是否准确。那么这样估计的准确性究竟如何呢?我们可以观察样本的方差:样本方差越大,这样估计的准确性就越低,且越不稳定。
说明:
文中提到的“样本”概念,其本身是可以由多个单元组成的,我们称单个样本所含的单元总数为样本容量。比如:把“所有中国人的身高”视为一个总体,从中随机取一百个人的身高。对于总体来说,这一百个人的身高数据就是它的一个样本。而某一个样本中个体数量就是样本容量。注意:不能说样本的数量就是样本容量,因为总体中的若干个个体只组成一个样本,样本容量不需要带单位。
然而光有方差或标准差(standard deviation)还是没有太大意义,为了真正地摸清样本均值与总体均值的相关性,我们需要去计算标准误差(Standard Error),它常被被用来度量基于不同样本得到的样本均值间的方差(离散程度)。
注意:计算标准误差是建立在以下假设条件之上:
1、样本是无偏的且服从正态分布
2、样本间是相互独立
如果假设无法满足,标准差也将不再准确。有很多方法用来进行检验并作出修正。标准差的计算公式为:
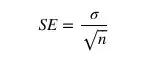
公式中,σ 是样本标准差,n是样本数量。

在Scipy的Stats库中,提供了内建的标准误差的函数。这个函数默认进行自由度修正,通常不需要启用(对于足够大的样本,自由度的修正实际上显得无关紧要)。你可以把ddof这个参数设置为0来关闭修正。

拓展:
standard deviation 是标准差,表示一组数值之间的离散程度,计算公式为:

standard error 是标准误,是样本统计量的标准差,这里说的统计量,包括但不限于平均数,标准差,方差,相关系数等。计算公式分为两部分:
1、总体标准差已知,公式为:

2、总体标准差未知,采用样本标准差的无偏估计,公式为:

注意,标准差与标准误差公式中的N和n含义不同。N代表的是样本容量,比如10个人为一组,样本容量就是10;而n代表的是样本统计量的数量,比如每10个人一个样本,重复采样20次进而对20个样本分别求得样本均值,就有20个“均值样本",那么n=20。
假设我们的数据是基于正态分布的,我们可以使用标准误差来计算“置信区间”。首先我们要做的,是预先确定我们期望达到的置信水平,比如95%。然后,我们要决定在正负几个标准差之内,能够达到这个置信水平。事实证明对于标准正态分布,95%的置信水平对应于正负1.96个标准差之内。当样本量足够大时(通常 > 30),中心极限定理便能派上用场,据此放心地做出样本是服从正态分布的假设。如果样本量偏小,一个更加谨慎的做法是,采用“指定适当的自由度的t分布”。实际应用中,可以根据累积分布函数来计算达到符合预期的置信区间,对应的标准差范围是多少。关于分布函数与累计分布函数以前的文章中也有过介绍,可以查看参考。现在让我们来演示一下如何通过Python 函数做检验。
注意:请谨慎应用中心极限定理,由于在金融领域中,许多数据都不是正态分布的。因此不考虑这些情况就随意地应用中心极限定理,将数据做正态分布的推断,是不被建议的。
以下是我们将95%的置信区间可视化以后的效果:







