目录
1 历史版本和工作界面
2 MATLAB命令的执行方式和编程
3 数值与符号计算
4 数据的可视化(工程与科学绘图)
5 M语言和工具箱
6 数据的分析与统计
7 Matlab优化
8 Simulink建模与仿真
MATLAB和Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB语言是以矩阵计算(所有的数据都是以数组的形式来表示和存储的)为基础的程序设计语言,它包含控制语句、函数、数据结构、输入和输出和面向对象编程特点。用户可以在命令窗口中将输入语句与执行命令同步,也可以先编写好一个较大的复杂的应用程序(M文件)后再一起运行。新版本的MATLAB语言是基于最为流行的C++语言基础上的,因此语法特征与C++语言极为相似,而且更加简单,更加符合科技人员对数学表达式的书写格式。使之更利于非计算机专业的科技人员使用。而且这种语言可移植性好、可拓展性极强,这也是MATLAB能够深入到科学研究及工程计算各个领域的重要原因。
MATLAB是一个包含大量计算算法的集合。其拥有600多个工程中要用到的数学运算函数,可以方便的实现用户所需的各种计算功能。函数中所使用的算法都是科研和工程计算中的最新研究成果,而且经过了各种优化和容错处理。在通常情况下,可以用它来代替底层编程语言,如C和C++ 。在计算要求相同的情况下,使用MATLAB的编程工作量会大大减少。MATLAB的这些函数集包括从最简单最基本的函数到诸如矩阵,特征向量、快速傅立叶变换的复杂函数。函数所能解决的问题其大致包括矩阵运算和线性方程组的求解、微分方程及偏微分方程的组的求解、符号运算、傅立叶变换和数据的统计分析、工程中的优化问题、稀疏矩阵运算、复数的各种运算、三角函数和其他初等数学运算、多维数组操作以及建模动态仿真等。
MATLAB自产生之日起就具有方便的数据可视化功能,以将向量和矩阵用图形表现出来,并且可以对图形进行标注和打印。高层次的作图包括二维和三维的可视化、图象处理、动画和表达式作图。可用于科学计算和工程绘图。
新版本的MATLAB可以利用MATLAB编译器和C/C++数学库和图形库,将自己的MATLAB程序自动转换为独立于MATLAB运行的C和C++代码。允许用户编写可以和MATLAB进行交互的C或C++语言程序。另外,MATLAB网页服务程序还容许在Web应用中使用自己的MATLAB数学和图形程序。
MATLAB 产品族可以用来进行以下各种工作:
数值和符号计算:算术、方程、微积分等;
数值分析:求最大值、最小值、平均值等;
工程与科学绘图:数据和函数的可视化;
控制系统的设计与仿真;
数字图像处理技术;
数字信号处理技术;
管理与调度优化计算(运筹学);
建模与仿真;
1 历史版本和工作界面
1.1 历史版本
MATLAB 7(R14):2004开发的版本。
MATLAB 8.0(2012b版):在MATLAB Desktop 中,工具条取代了菜单和工具栏。
2014b版:推出了全新的 MATLAB 图形系统。全新的默认颜色、字体和样式便于数据解释。抗锯齿字体和线条使文字和图形看起来更平滑。图形对象便于使用 – 您可以在命令窗口中显示常用属性,并且对象支持熟悉的结构化语法,可以更改属性值。另外,还增加了许多其他新功能。
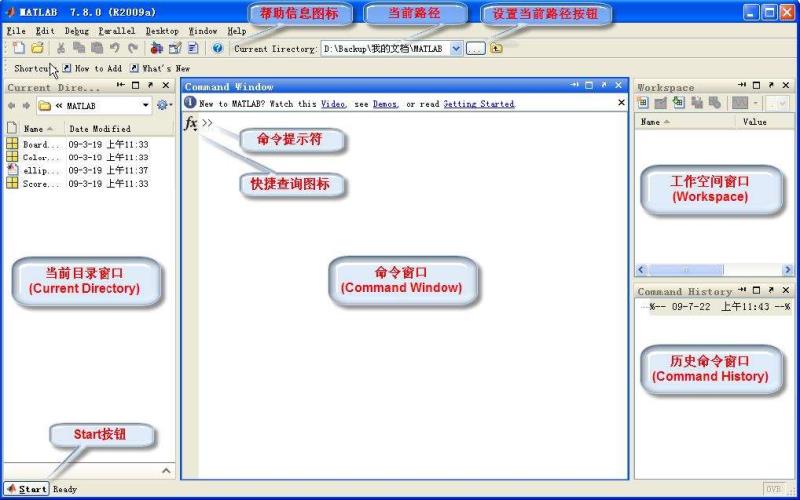
1.2 工作界面
I 命令窗口Command Window
MATLAB是交互式语言,输入命令即给出运算结果。指令窗口的常用功能主要包括算数运算、表达式运算、函数绘图、功能标点符、常用控制指令等。
II 工作空间Workspace
内存变量的指令操作和数据的文件存取。
III 历史指令窗口Command History
用于记录在指令窗口中运行过的所有指令,这些指令可以被复制,也可以送到指令窗口中再次运行。
IV 当前文件夹窗口Current Folder

MATLAB
7.8.0 R2009a
R2013a
Matlab是一个很多功能的软件,很多功能用不到,安装的时候就不要安装了, 这样启动的速度会快很多的。
2 MATLAB命令的执行方式和M语言编程
2.1 交互式命令的执行方式(命令窗口)
逐条输入,逐条执行,操作简单、直观,但速度慢,执行过程不能保留。
2.2 M文件的执行方式
将命令编成程序保存在一个文件中(M文件),依次运行文件中的命令,可以重复进行。M文件是由若干Matlab命令组成在一起构成的,它可以完成某些操作,也可以实现某种算法。
M文件根据调用方式的不同分为两类(扩展名都是.m):
I 命令文件Script File:没有输入参数,也不返回输出参数;命令文件对工作空间中的变量进行操作,文件中所有命令的执行结果也返回工作空间中。命令文件可以直接运行。
II 函数文件Function File:可以带输入参数,也可以返回输出参数;函数文件中定义的变量为局部变量,当函数文件执行完毕时,这些变量也被清除。函数文件不能直接运行,要以函数调用的方式来调用它。
2.3 M语言编程
利用M语言可以通过编写脚本或者函数文件实现用户自己的算法。
新建一个M文件,通过文件-新建,或者通过快捷方式都可以,然后,在M文件中输入如下代码:
function [a,b]=example(x1,x2)
a=x1;
b=x1+x2;
我们完成了函数的编写。
在MATLAB主窗口中输入如下命令;[a,b]=example(1,2),回车。
我们可以看到如下结果:
a =1 b=3,我们完成了函数的调用。
求一元二次方程ax²+bx+c=0的根
a=input(‘a=?’);
b=input(‘b=?’);
c=input(‘c=?’);
d=b*b-4*a*c;
x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)];
disp([‘x1=’,num2str(x(1)),’,x2=’,num2str(x(2))]);
程序输出为:
a=?4
b=?78
c=?54
x1=-0.7188,x2=-18.7812
求[100,200]之间第一个能被21整队的整数。
for n=100:200
if rem(n,21)~=0;
continue
end
break
end
n
程序输出结果为:
n=
105
3 数值与符号计算
3.1 数值计算
数值计算主要指数值数组及矩阵的运算。
>>1-sin(pi/2)+100*(1-3^2)
ans=
-800


3.2 符号计算
MATLAB为符号计算提供了一种引入符号对象的数学运算工具箱,包含函数的复合、简化、极限、积分、泰勒展开式、级数求和,以及求解代数方程和微分方程等函数命令。
如求y=x³+x²+x+1的导数:
>>syms x
>>y=x^3+x^2+x+1
>>D1=iff(y)
D1=3*x^2+2*x+1

4 数据的可视化(工程与科学绘图)
下面举一个简单的例子,绘制余弦曲线y=sinx。
4.1 产生工作区变量
在命令行窗口中输入命令:
>>x = 0:pi/100:2*pi; %在区间[0,2π]中插入间隔为π/100的点
>>y=sin(x); %计算对应x的点的函数值
运行后,则在”Workspace”中显示内存变量x和y。
4.2 变量选定
在”Workspace”中,单击所需绘图的变量x和y,由x和y在工具栏左边显示。
4.3 绘图
选择“PLOTS”选项卡中的相应选项,绘制区域图:
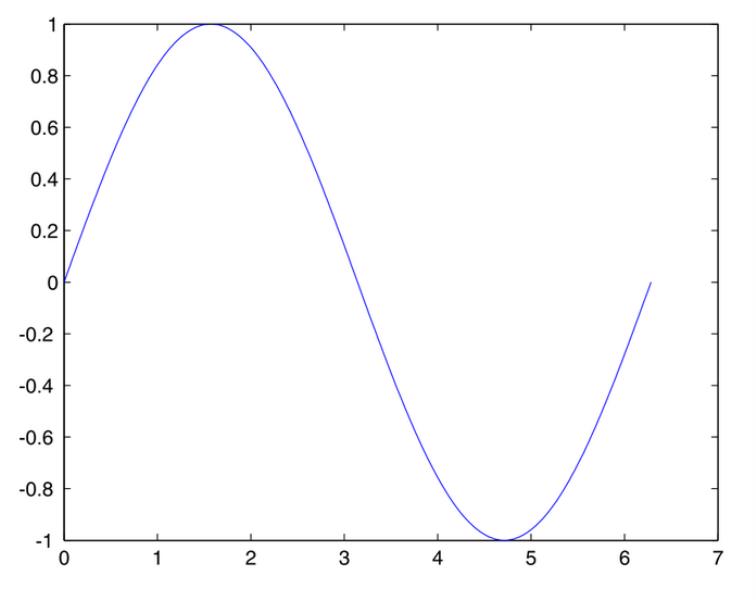
5 M语言和工具箱
MATLAB提供了基本的数学算法,例如矩阵运算、数值分析算法,也集成了2D和3D图形功能,以完成相应数值可视化的工作,并且提供了一种交互式的高级编程语言-M语言,利用M语言可以通过编写脚本或者函数文件实现用户自己的算法。
利用M语言还开发了相应的MATLAB专业工具箱函数供用户直接使用,这些工具箱应用的算法是开放的、可扩展的,用户不仅可以察看其中的算法,还可以针对一些算法进行修改,甚至允许开发自己的算法以便扩充工具箱的功能。目前MATLAB产品的工具箱有40多种,分别涵盖了数据获取、科学计算、控制系统设计与分析、数字信号处理、数字图像处理、金融财务分析以及生物遗传工程等专业领域。
MATLAB的一个重要特色就是具有一套程序扩展系统和一组称之为工具箱的特殊应用子程序。工具箱是MATLAB函数的子程序库,每一个工具箱都是由特定领域的专家开发的、为某一类学科专业和应用而定制的,主要包括信号处理、控制系统、神经网络、模糊逻辑、小波分析和系统仿真等方面的应用。
6 数据的分析与统计
在经营管理活动中,往往会产生大量的统计数据,对这些数据进行科学分析,可以提高管理决策水平。
数据分析是用适当的统计方法对各种数据加以详细研究和概括总结的过程,已成为当代自然科学和社会科学各个学科研究者必备的知识。matlab是一套高性能的数值计算和可视化软件,是实现数据分析与处理的有效工具。数据分析主要内容包括:数据描述性分析、回归分析、判别分析、主成分分析与典型相关分析、聚类分析、数值模拟分析等。
7 Matlab优化
在生活中,人们对于同一个问题往往会提出多个解决方案,并通过各方面的论证从中提取最佳方案。例如:对于工厂企业而言,如何在消耗总工时最小的情况下获取最大的产品数量?如何安排物流秩序,在满足最大效率的前提下,达到成本最低、运费最小?最优化方法就是专门研究如何从多个方案中科学合理地提取出最优方案的技术。
利用Matlab的优化工具箱,可以求解线性规划、非线性规划和多目标规划问题。具体而言,包括线性、非线性最小化、最大化,二次规划,曲线拟合,半无限问题,线性、非线性方程(组)的求解,线性、非线性的最小二乘等问题。
7.1 建立数学模型:即用数学语言来描述最优化问题。模型中的数学关系式反映了最优化问题所要达到的目标和各种约束条件。
7.2 数学求解:数学模型建立好后,选择合理的最优化方法进行求解。
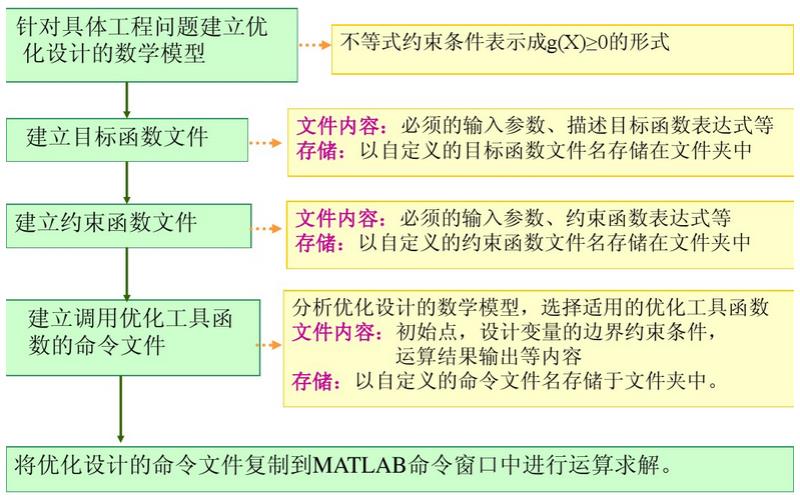
优化的一般步骤
8 Simulink建模与仿真
Simulink是Simulation(模拟仿真)和Link(连接)的组合词。
Simulink提供一个动态系统建模、仿真和综合分析的集成环境。在该环境中,无需大量书写程序,而只需要通过简单直观的鼠标操作,就可构造出复杂的系统。
Simulink是用于动态系统和嵌入式系统的多领域仿真和基于模型的设计工具,对各种时变系统,包括通信、控制、信号处理、视频处理和图像处理等系统,Simulink提供了交互式图形化环境和可定制模块库来对其进行设计、仿真、执行和测试。
Simulink可以提供研究对象的建模、仿真和分析,使用图形化的系统模块对研究对象进行描述,每个模块就像实验室中的一台仪器,可以根据需要进行不同的组合以达到不同的研究目的。
在Simulink中,模块是仿真的基石,将这些模块相连接构成系统,就可以进行仿真,运行结果可以用图形的形式显示出来,整个仿真过程非常简洁、方便、直观。