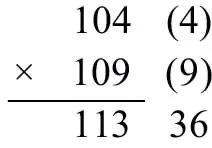
这个发现让我非常开心,尽管我并不是发现这个规律的第一人。当时,我正在求解和为20的两个数字(例如10和10,9和11)的最大乘积。我发现,当这两个数字都是10时,它们的乘积可能是最大的。结果,下图揭示的规律证实了我的猜想。

和为20的两个数字的乘积
这个规律没有任何错误。随着两个数字
之间的差不断增大,它们的乘积却越来越小。这些乘积与100的差是多少呢?答案是1、4、9、16、25,也就是1^2、2^2、3^2、4^2、5^2,以此类推。这个规律是不是始终有效呢?我决定验证一下和为26的两个数字是否也符合这个规律。

和为26的两个数字的乘积
同样,当这两个数字相等时,它们的乘积最大,而且这些乘积与169的差依次为1、4、9,等等。在验证了几次之后,我确信这个规律是正确的。(我会在下文中用代数方法证明它。)然后我发现,我可以用这个规律快速地完成平方运算。
假设要计算13的平方数。我们无须直接计算13 × 13,而可以进行更简单的计算:10×16 = 160。这个得数与正确答案已经非常接近了。由于这两个因数与13分别相差3,因此还需要在它们乘积的基础上加上3^2。即
132 =(10×16) 32 = 160 9 = 169
再试一次,利用这个方法计算98 × 98。一个因数加上2等于100,另一个因数减去2等于96,在100×96的乘积基础上加上2^2。即
98^2 =(100×96) 2^2 = 9 600 4 = 9 604
如果某个数的个位数是5,进行平方运算时就会特别简单,因为该数字分别加、减5之后,两个因数的个位数都是0。例如:
352 =(30×40) 5^2 = 1 200 25 = 1 225
552 =(50×60) 5^2 = 3 000 25 = 3 025
852 =(80×90) 5^2 = 7 200 25 = 7 225
现在,试试看如何计算59^2。因数59分别加、减1之后,算式就变为:59^2 = (60 × 58) 12。但是,60 × 58怎么心算呢?答案是:由左至右。先忽略60后面的那个0,用从左至右的方法计算6 × 58:6 × 50 = 300,6 × 8 = 48。然后,把这两个数字(从左至右)相加,得到348。因此,60 × 58 = 3 480。那么
59^2 =(60×58) 1^2 = 3 480 1 = 3 481
延伸阅读
下面,我们通过代数运算来解释其中的道理。
A^2 = (A d) (A–d) d^2
其中A是平方运算的底数,d是A与离其最近的简便数字的差(当然,d取任意值时,上述公式都成立)。例如,计算59的平方数时,A = 59,d = 1。根据公式,计算(59 1)×(59–1) 1^2就可以得出答案。
在你对两位数的平方运算感到得心应手之后,还可以利用这个方法完成三位数的平方运算。例如,如果我们知道12^2 = 144,那么
112^2 = (100×124) 12^2 = 12 400 144 = 12 544
如果乘法运算中的两个因数都与100接近,就可以利用类似方法完成计算。第一次看到这个方法时,大家都会觉得它很神奇。
以104×109为例。如下图所示,我们在每个数字旁边写上该数字与100的差。然后,将第一个数字与第二个差相加,即104 9 = 113。再将两个差相乘,即4×9 = 36。最后,将这两个运算步骤的得数写到一起,答案就会神奇地出现在你的眼前。
看着数字的这些规律,有人禁不住会问:“这些规律确实很有意思,但是它们有什么用处呢?”对于这样的问题,任何艺术家都会嗤之以鼻,因为在他们眼中,这些优美的规律本身就是一种美!大多数数学家也会有同样的反应。而且,对这些规律的理解越深入,就越能体会其中蕴藏的美。有的规律不仅优美,还可以用来解决某些实际问题。
,






